Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 7

Основные положения

Большинство величин, с которыми имеет дело исследователь в эконометрике, являются не жестко детерминированными, а вероятностными величинами. Мы можем лишь оценить их значения, предположить с определенной вероятностью границы, в которых они могут находиться на самом деле. Это связано с объективно существующими ошибками наблюдения.

Для описания случайных величин используют две основные характеристики:

1.  ожидаемое значение

2.  меру разброса значений (как правило, дисперсию)

Случайная величина записывается в виде: , где μ – математическое ожидание случайной величины, а ε – чисто случайная составляющая (остаток).

Необходимо отметить, что оценкой в эконометрике называют как формулу, по которой происходит процесс оценки, так и само значение, полученное по этой формуле.

Все статистические показатели: показатели центральной тенденции, показатели вариации, показатели связи, а также параметры регрессионных уравнений имеют как теоретические, существующие «на самом деле» значения, так и выборочные значения, определяемые на основе ограниченного массива данных и являющихся по сути, оценками теоретических величин:

Обычно теоретические значения обозначаются греческими буквами, а их оценки, полученные в результате эмпирического анализа – соответствующими латинскими.

Для проведения оценки случайных величин используются специальные методы: методы выборочного наблюдения и интерпретации его результатов, метод статистической проверки гипотез.

Существует два типа оценок – точечные и интервальные.

Точечная оценкапредставляет собой конкретное число, которое используется в качестве характеристики случайной величины. Она не дает точного представления о распределении показателя, однако определяет их наиболее вероятные значения. Основные формулы точечной оценки представлены в таблице 2.1

Таблица 2.1

Основные формулы точечной оценки

* – формула оценивания параметра регрессионной модели приведена для случая линейной регрессии

При оценке качества точечных оценок анализируются четыре основных свойства оценок:

1.  Несмещенность;

2.  Эффективность;

3.  Состоятельность;

4.  Достаточность.

Точечное значение параметра генеральной совокупности называется несмещенным, если математическое ожидание значения оценки равно истинному значению параметра, другими словами, если оценки располагаются симметрично относительно истинного значения характеристики генеральной совокупности (рис. 2.1).

Математически это свойство записывается следующим образом: .

Оценка называется эффективной, если она максимально точно описывает истинное значение, то есть мера разброса точечных оценок, получаемых в различных наблюдениях, минимальна (рис. 2.2)

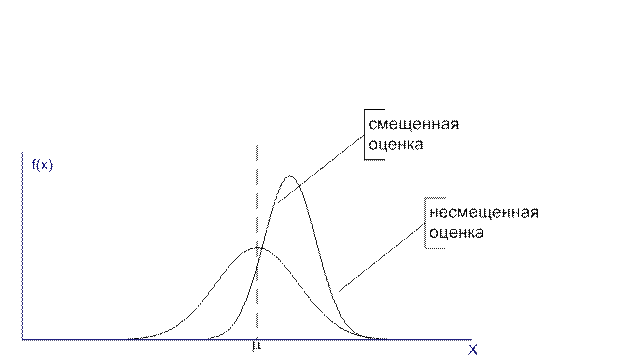
Рис. 2.1 Несмещенность статистической оценки

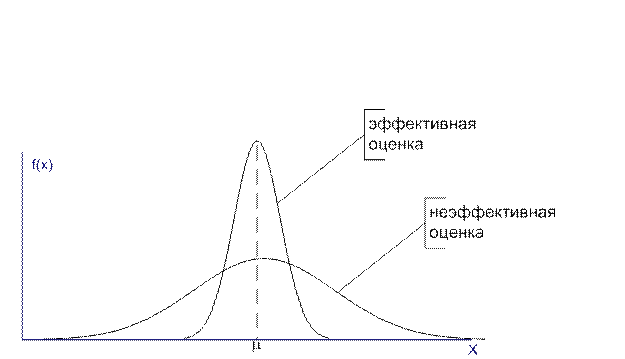
Рис. 2.2 Эффективность статистической оценки

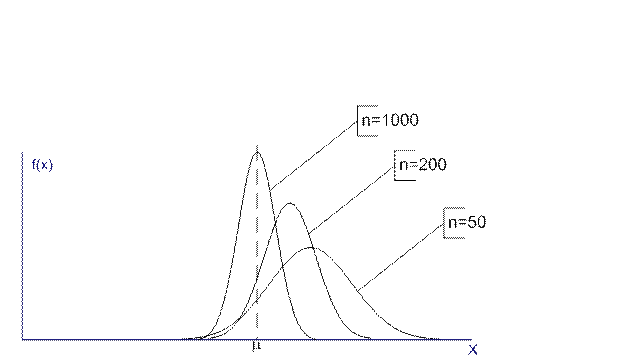
Рис. 2.3 Состоятельность статистической оценки

Часто перед исследователем возникает проблема выбора между эффективной и несмещенной оценками. Выбор в пользу несмещенной оценки делается в том случае, если возможные ошибки не сильно беспокоят исследователя при условии их взаимной компенсации. Если же большие ошибки недопустимы, то выбор будет сделан в пользу эффективной, но смещенной оценки.

Оценка является состоятельной, если по мере увеличения числа единиц в анализируемой выборке ее значение стремится к истинному значению показателя (рис. 2.3).

Под достаточностью понимают такое свойство точечной оценки, согласно которому для ее проведения используется максимум информации.