Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 16

Для статистически значимого коэффициента детерминации может быть проведена интервальная оценка при помощи z-распределения Фишера. Порядок оценки следующий: рассчитывают величину , и для нее проводят оценку по тому же алгоритму, что и для коэффициента корреляции (см. тему 2). Затем полученные значения доверительных пределов возводятся в квадрат и получаем искомую интервальную оценку.

II. Анализ точности определения оценок регрессии осуществляется путем вычисления дисперсий коэффициентов регрессии. Для линейной регрессионной модели  значения выборочных дисперсий будут равны:

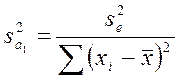                                                                         (3.30)

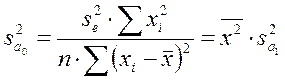                                                       (3.31)

Таким образом, оценки коэффициентов будут тем точнее, чем меньше значение необъясненной дисперсии.

Значения дисперсий коэффициентов регрессии и корни квадратные из них – стандартные ошибки коэффициентов регрессии – используются на следующем этапе для проверки статистической значимости коэффициентов регрессии.

III. Оценка статистической значимости коэффициента регрессии осуществляется путем проверки гипотезы о равенстве этого коэффициента 0. Для коэффициента a₁ такая гипотеза будет иметь вид:

H₀ : a₁ = 0

H₁ : a₁ ≠ 0

Для проверки этой гипотезы пользуются t-статистикой:

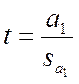                                                                                          (3.32)

это соотношение имеет распределение Стьюдента с числом степеней свободы, равным (n –2). Расчетное значение tсравнивают с критическим 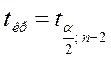, взятым из таблицы (ПРИЛОЖЕНИЕ 2) где α – уровень значимости. Если фактическое значение оказывается больше критического, то нулевая гипотеза отвергается, и делается вывод о статистической значимости коэффициента регрессии. В противном случае считается, его значением можно пренебречь, и рассматривать модель с меньшим числом параметров.

Для предварительной «грубой» оценки статистической значимости коэффициентов регрессии можно пользоваться следующим правилом:

Таблица 3.2

Правило «грубой» оценки статистической значимости
коэффициентов регрессионного уравнения

Это правило позволяет достаточно точно установить значимость коэффициентов регрессии при n >10.

IV. Интервальная оценка коэффициентов регрессионного уравнения осуществляется для того, чтобы получить более полное представление о характере регрессионной зависимости между переменными. Ее результатом будут доверительные интервалы для каждого коэффициента:

для α₀ – 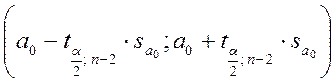                                (3.33)

для α₁ – 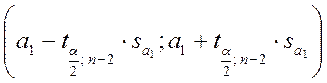                                 (3.34)

Доверительный интервал определяет границы, в которых будет находиться значение теоретического коэффициента регрессии с уровнем значимости α.

Уровень значимости α определяется исходя из требуемой точности. Обычно – 0.1, 0.05 или 0.01.

V. Расчет доверительных интервалов для зависимой переменной позволяет решить две задачи: во-первых, провести интервальную оценку математического ожидания зависимой переменной для конкретного значения независимой переменной и заданного уровня значимости, и, во-вторых, определить границы, за пределами которых может оказаться не более чем α-ая доля индивидуальных значений зависимой переменной для конкретного значения независимой переменной.

Первая задача решается путем нахождения доверительного интервала для зависимой переменной по формуле:

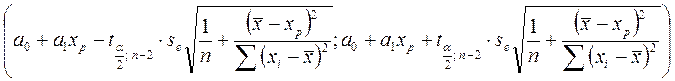   (3.35)

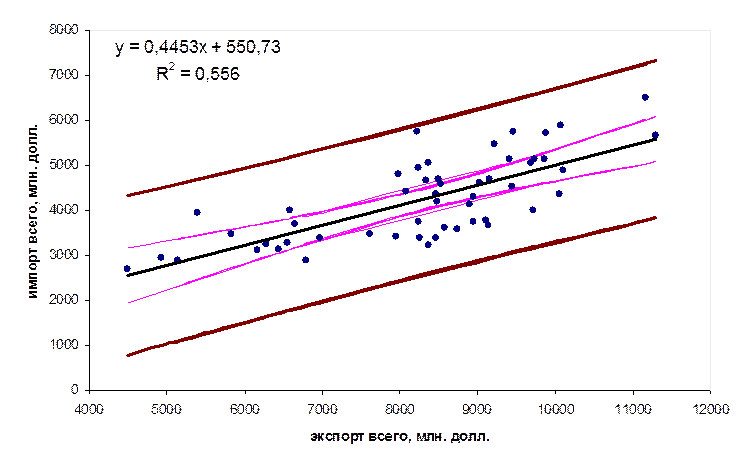
Для каждого значения x_p из области, в которой находятся значения независимой переменной, определяются доверительные интервалы. Они будут наименьшими при  и увеличиваться по мере удаления от среднего значения (рис. 3.5).