5. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. Учебное пособие. 2-е изд. – М.: Дело, 1998. – с. 69 – 74
6. Практикум по эконометрике: Учебное пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – с. 49 – 105
7. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2002. – с.141 – 155
6.1 Временной ряд. Стационарные и нестационарные временные ряды
6.2 Динамические модели с лагами в независимых переменных
6.3 Авторегрессионные динамические модели: методы распознавания и учета
6.4 Проблема автокорреляции остатков и методы ее преодоления
6.5 Особенности определения трендовой составляющей
6.6 Методы анализа циклической составляющей в динамических моделях
6.7 Учет в динамических моделях влияния различных факторов.
6.8 Прогнозирование при помощи регрессионных динамических моделей
Динамической регрессионной моделью называется регрессионная модель, в которой в качестве объясняющих переменных используются не только текущие, но и предшествующие значения, а также временной фактор. Динамические регрессионные модели строятся по данным из временных рядов (рядов динамики) – последовательности данных, характеризующих состояние объекта в различные моменты времени.
Различают стационарные и нестационарные временные ряды. В стационарных временных рядах вероятностные характеристики анализируемого показателя не меняются со временем. В таких рядах колебание зависимой переменной обусловлено действием всевозможных факторов, либо совершенно не связанных со временем (например, изменение величины экспорта во времени может зависеть от валютных курсов), либо взаимосвязь эта имеет периодический характер (величина экспорта может достаточно сильно колебаться в зависимости от времени года).
Другими словами, свойства строго стационарного временного ряда не меняются при изменении начала отсчета времени. В частности, из предположения о строгой стационарности временного ряда xt следует, что закон распределения вероятностей случайной величины xt не зависит от t, а значит, не зависят от t и все его основные числовые характеристики, в том числе: среднее значение M(xt) = mи дисперсия D(xt) = s2.
В нестационарных временных рядах анализируемый признак имеет определяемую временем устойчивую тенденцию изменения. Соответственно, все характеристики нестационарного временного ряда зависят от фактора времени.
Динамические регрессионные модели бывают различных видов (см. рис. 6.1)
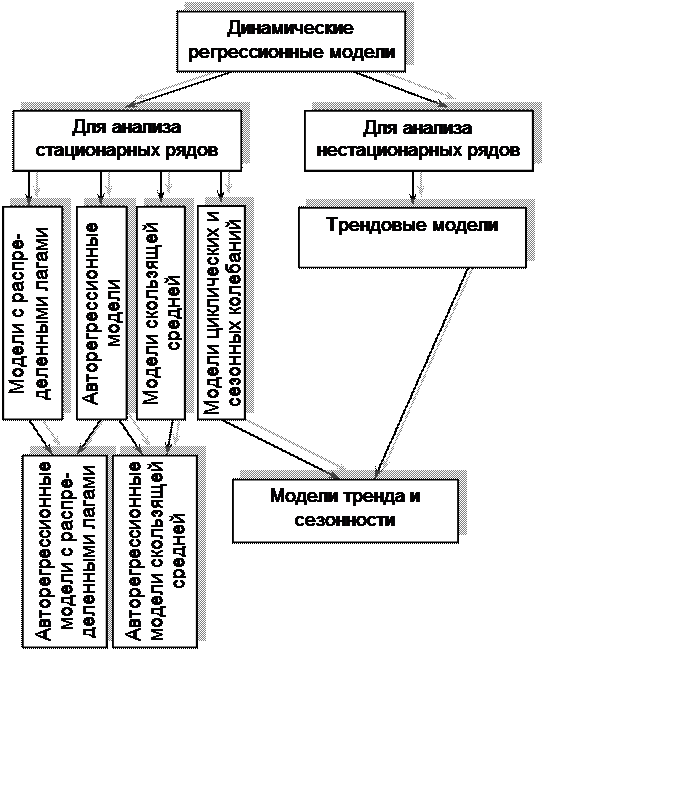
Рис. 6.1 Типология динамических регрессионных моделей
Большинство эконометрических моделей разработаны для анализа стационарного ряда, поскольку методы его анализа значительно проще, а нестационарный ряд достаточно легко приводится к стационарному путем исключения основной временной тенденции (тренда). Более подробно об анализе основной тенденции и колебательных (сезонных) процессов в ряде динамики можно прочитать в учебниках по статистике и в специализированной литературе. Для нас особый интерес представляют факторные динамические модели, в которых в качестве объясняющих переменных используются переменные, принадлежащие различным периодам времени.
В том случае, если в качестве объясняющих переменных используются значения результативной переменной в предыдущие периоды, то такая модель называется авторегрессионной.
Переменные, отражающие значения факторов в предшествующие периоды, называются лаговыми переменными. Временные лаги (запаздывание реакции зависимой переменной на изменение факторов) существуют в экономике по следующим причинам:
1. Психологические причины. Сюда, в первую очередь, входит инерция в поведении людей, связанная с адаптивными ожиданиями.
2. Технологические причины. К примеру, действие фактора НТП не приведет к мгновенному росту, поскольку внедрение новых технологий – достаточно длительный по времени процесс. Точно также инвестиции, направленные в отрасль, дадут отдачу только через некоторое время.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.