, (3.10)
(3.11)
в том случае, если расчет выполнен по формуле (3.10), говорят о методе наименьших квадратов (МНК), если по формуле (3.11) – о методе наименьших модулей (МНМ).
Результаты сравнительного анализа этих методов приведены ниже:
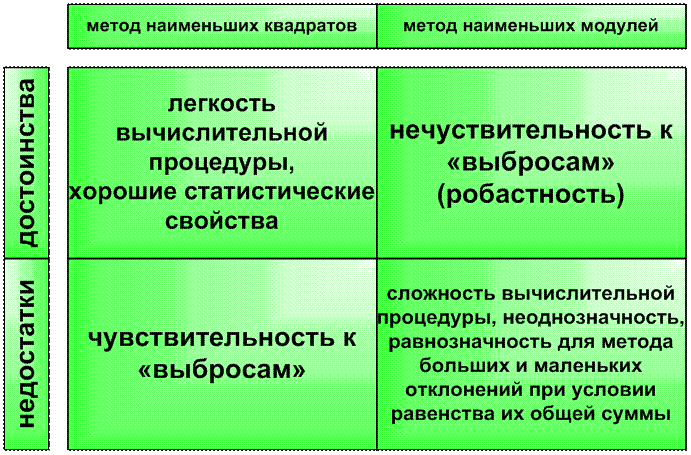
Рис. 3.2 Сравнительный анализ основных математических методов определения параметров уравнения регрессии.
Для совмещения достоинств этих методов разработана более сложная кусочно заданная функция Хубера :
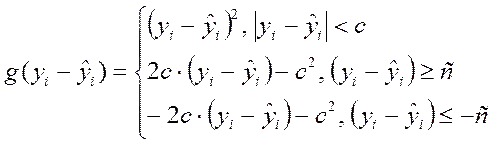(3.12)
где с – параметр, показывающий границу, начиная с которой в качестве меры отклонения используется модуль (при меньших – квадрат), чем он больше, тем сильнее чувствительность .
Для снижения чувствительности g() к выбросам (значениям, выбивающимся из общей тенденции) Пиндайк и Рубинфелд ввели функцию:
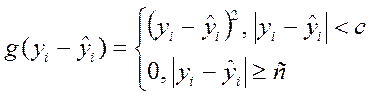(3.13)
Рассмотрите сущность и особенности применения метода максимального правдоподобия
Наибольшее распространение в настоящее время получил метод наименьших квадратов. Рассмотрим условия применения МНК, основной алгоритм расчета параметров и свойства оценок параметров, полученных в результате его применения.
Условия применения (предпосылки) МНК (условия Гаусса – Маркова).
1. Математическое ожидание случайного отклонения равно 0 для всех наблюдений: M(ε)=0
2.
Дисперсия случайных отклонений
постоянна: 
3. Случайные отклонения независимы друг от друга:
4.
Случайное отклонение независимо от
объясняющих переменных регрессионной модели: 
5. Модель линейна относительно параметров
Математически условие минимизации квадратов отклонений запишется следующим образом:
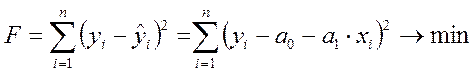(3.14)
найдем минимум F относительно a0 и a1, вычислив частные производные F по a0 и a1 и прировняв их к 0:
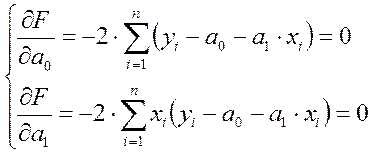(3.15)
преобразуем полученную систему:
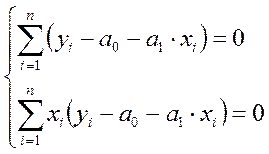, (3.16)
раскрыв скобки, получаем стандартную форму нормальных уравнений для вычисления коэффициентов линии регрессии.
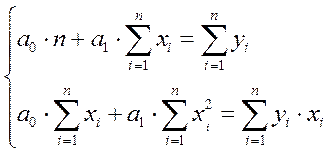(3.17)
решив это уравнение относительно a0 и a1 , получим оценки параметров теоретического уравнения α0 и α1, обладающие всеми основными свойствами качественных оценок: (по теореме Гаусса-Маркова): несмещенность, эффективность, состоятельность. Это обуславливает широкое использование МНК в эконометрических расчетах.
Для линейной модели существует упрощенный способ расчета параметров, основанный на решении системы (3.14)
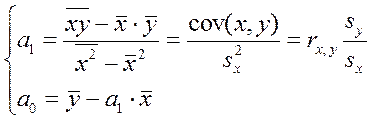(3.18)
Однако не все фактические данные могут быть описаны при помощи линейной модели. В этом случае используется нелинейная регрессия. Для того, чтобы определить, какую аналитическую форму регрессионной модели выбрать, используют следующий алгоритм (применяется для каждой гипотезы об определенной аналитической форме регрессии) (рис. 3.3). Следует отметить, что этот алгоритм применим только в случае монотонной зависимости между факторами.
Рис. 3.3 Алгоритм определения аналитической формы регрессии
Расчет параметров нелинейных регрессионных моделей основан на том же методе, что и для линейной регрессии. Основное требование – уравнение регрессии должно быть либо линейно относительно параметров, либо преобразуемо в такое уравнение (это преобразование называется линеаризацией). В случае параболической модели и полиномиальной модели более высокой степени система уравнений для определения параметров претерпевает очевидные изменения (3.20):
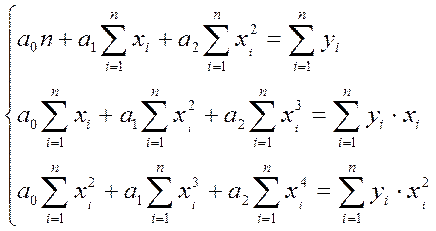, (3.20)
где a0, a1 и a2 – оценки параметров в
уравнении регрессии 
В случае линеаризации происходит замена переменных в уравнении регрессии с тем, чтобы привести его к линейному виду. Обратите внимание, что линеаризованы могут быть функции с числом параметров, равным числу параметров в соответствующей линейной модели (для парной регрессии – с двумя параметрами), поэтому по сравнению с таблицей 1.1 аналитические выражения для основных функций претерпели определенные изменения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.