Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 49

y=α₀ + α₁x₁ + ε

3.  Оценка параметров модели. Проведем оценку параметров модели при помощи различных способов.

3.1  Метод средних. Предположим, что изменение сбережений обусловлено только изменением денежных доходов (т.е. α₀ = 0). Тогда оценка a₁ неизвестного параметра α₁ определится по формуле (3.5):

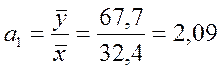
модель принимает вид: y=2,09x₁+e

3.2  Метод проб. В августе прирост денежных доходов был практически нулевым, при этом прирост сбережений составил 64,6 млрд. руб. Можно предположить, что это значение характеризует нулевой уровень зависимой переменной, т.е. ее значение, обусловленное действием прочих факторов. Тогда по формуле (3.6) рассчитаем оценку параметра α₁:

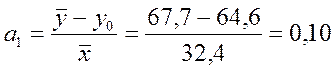
в этом случае уравнение регрессии примет вид:

y=64,6+0,10x₁+e

3.3  Метод выбранных точек. Проанализируем корреляционное поле и выберем точки, которые ближе всех лежат в предполагаемой прямой линии, описывающей модель. Это будут точки «сентябрь»
(–18,9;46,0) и «декабрь» (162,4;124,0).

Рассчитаем параметры модели по формулам (3.7) и (3.8):

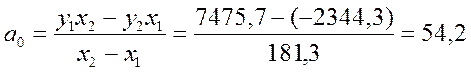
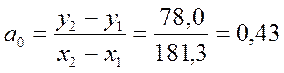
уравнение регрессии выглядит следующим образом:

y=54,2+0,43x₁+e

3.4  Метод наименьших квадратов. Для применения этого метода составим вспомогательную таблицу:

Составим систему для расчета значений параметров:

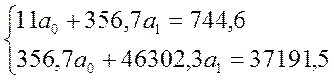
Решив эту систему, получаем значения

a₀=55,5

a₁=0,38

Линия регрессии описывается уравнением: y=55,5+0,38x₁+e

Сведем полученные результаты в таблицу:

Таблица 3

Уравнения регрессий, полученные при помощи разных методов

Покажем на графике различие между полученными линиями регрессии:

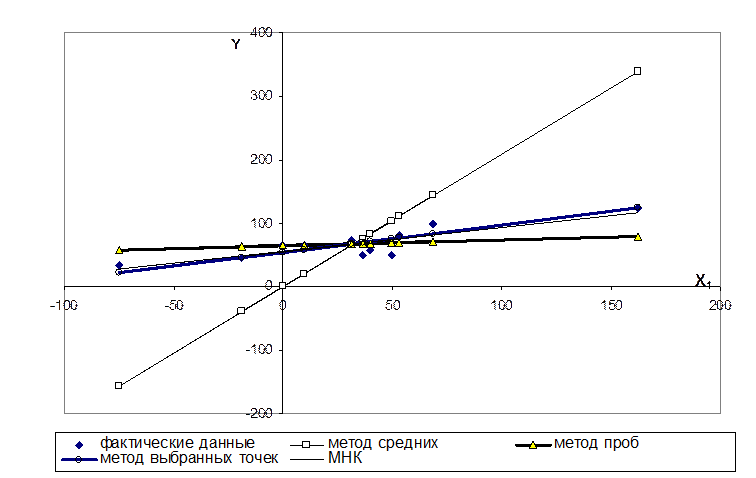
Рис. 2 Линии регрессии, полученные при помощи различных методов

4.  Проверка качества построенной модели. Выполним оценку качества поэтапно.

4.1.  Оценку адекватности модели в целом проведем для каждой из выбранных моделей:

Таблица 4.

Предварительные расчеты для вычисления
дисперсий случайных отклонений