Экономика и менеджмент \ Эконометрика

Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 21

Оценка качества построенной модели проводится по тем же этапам, что и для парной регрессии (см. рис. 3.4):

1.  Анализ адекватности модели в целом

2.  Анализ точности определения оценок коэффициентов регрессии (расчет их дисперсии и стандартного отклонения)

3.  Проверка статистической значимости коэффициентов регрессии

4.  Интервальная оценка коэффициентов регрессионного уравнения

5.  Определение доверительных интервалов для зависимой переменной

Логика всех этапов аналогична парной регрессии.

1. Оценка адекватности модели в целом осуществляется на основе расчета коэффициента детерминации  (см. формулы 3.26 – 3.28) и скорректированного коэффициента детерминации , рассчитываемого по формуле:

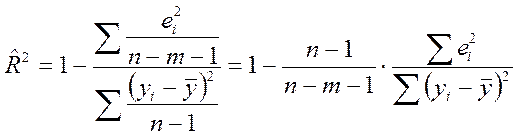                (4.9)

После несложных преобразований получаем выражение для  через :

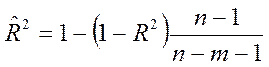                                                          (4.10)

из последней формулы видно, что скорректированный коэффициент детерминации меньше обычного коэффициента детерминации и, следовательно, является более строгим показателем связи, чем .

Отметим, что корректировка может производиться, только если выполняется соотношение:

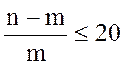                                                                                  (4.11)

После определения значения коэффициента детерминации следует проанализировать его статистическую значимость. Статистическая значимость проверяется путем проверки гипотезы о равенстве коэффициента детерминации 0. Если гипотеза отвергается, то делается вывод о том, что коэффициент детерминации отличен от 0 и статистически значим. Для проверки используют F-статистику:

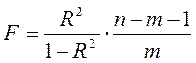                                                                      (4.12)

Полученное фактическое значение сравнивают с критическим Fα; m; n-m-1, если оно оказывается больше критического, то нулевая гипотеза отвергается и делается вывод о статистической значимости коэффициента детерминации и существенности построенной модели. В противном случае модель нельзя использовать на практике.

Для множественной регрессии оценка качества модели в целом также может осуществляться с использованием средней ошибки аппроксимации:

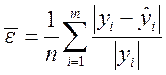                                                                           (4.13)

Если значение  превышает 0,15 (15%), то модель недостаточно хорошо описывает фактические данные.

2. Расчет дисперсии коэффициентов регрессионного уравнения. Точный расчет производится с использованием элементов матричной алгебры и отводится на самостоятельное изучение. Приближенное же вычисление дисперсии можно осуществить по формуле:

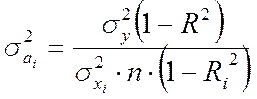                                                            (4.14)

где Ri –коэффициент полной корреляции i-й переменной с остальными независимыми переменными (может быть определен как корень квадратный коэффициента детерминации регрессионной модели , где j не равно i).

Покажите, при помощи каких расчетов оценивается статистическая значимость параметров уравнения множественной регрессии и строится доверительный интервал для зависимой переменной?

Рассмотрим одну из существенных проблем, возникающих при применении множественного регрессионного анализа – мультиколлинеарности. Под мультиколлинеарностью понимают тесную линейную взаимосвязь объясняющих переменных (рис. 4.1 и 4.2). Термин мультиколлинеарность введен Р. Фришем.

Рис. 4.1 Мультиколлинеарность между x1 и x2
a) мультиколлиенеарности нет; b) умеренная мультиколлиенарность;
с) сильная мультиколлинеарность;
d) совершенная мультиколлинеарность

В случаях, проиллюстрированных на рис. 4.1 a) и b) в модель можно включать обе независимые переменные, а в случаях с) и d) –только одну из двух переменных.

Проблема мультиколлинеарности связана, прежде всего, со следующими ее последствиями (рис. 4.2).

1.  Высокие значения дисперсии оценок коэффициентов, что приводит к ухудшению точности их интервальных оценок, а также уменьшению t-статистик коэффициентов, что может привести к неправильному выводу о несущественности влияния независимой переменной на зависимую.

Скачать файл