3. Институциональные причины. Большинство соглашений в экономике имеют фиксированный срок действия, и отказаться от них, даже в случае изменения внешних факторов, затруднительно.
4. Методы расчета анализируемых показателей. Такие показатели, как уровень инфляции, уровень безработицы, денежный мультипликатор и т.п. изначально определяются как функции от переменных, принадлежащих к различным временным периодам
Для определения наличия лагов в авторегрессионных моделях используют коэффициент автокорреляции, который характеризует силу и направление связи между членами одного временного ряда, отстающими друг от друга на фиксированный временной период.
Статистической оценкой коэффициента автокорреляции является выборочный коэффициент автокорреляции (6.1):
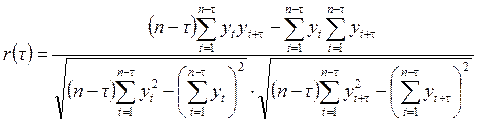(6.1)
где τ – временной лаг, для которого определяется корреляция.
Фактически выборочный коэффициент автокорреляции можно представить как коэффициент корреляции между членами одного временного ряда:
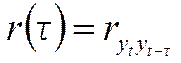(6.2)
Выборочный коэффициент автокорреляции обычно вычисляется для временных лагов, не превышающих четверти выборки, то есть τ≤ n/4. График зависимости r(τ) называется коррелограммой. В модель обычно включают переменные, соответствующие лагам с высокими по абсолютному значению выборочными коэффициентами автокорреляции (рис. 6.2).
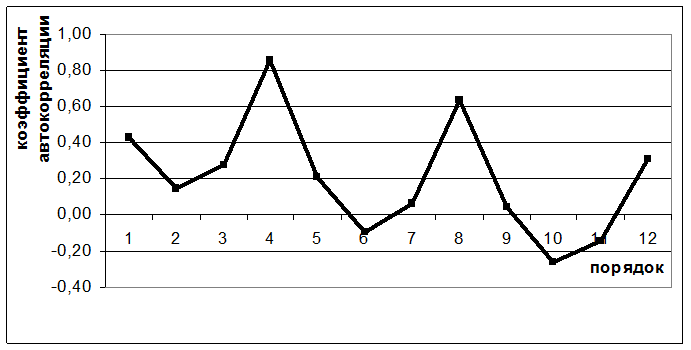
Рис. 6.2 Кореллограмма, построенная по квартальным данным (заметна сильная положительная корреляция между каждым четвертым кварталом)
С точки зрения спецификации факторные динамические модели, используемые для анализа стационарных рядов, бывают различных видов:
1. Модели с распределенными лагами p-го порядка (DL(p)) – модели, в которых учитываются только лаги в независимых переменных:
(6.3)
2. Авторегрессионная модель p-го порядка (AR(p)) – это динамическая регрессионная модель, в которой в качестве объясняющих переменных используются значения зависимой переменной за p предшествующих периодов.
(6.4)
3. Модель скользящей средней q-го порядка (MA(q)) – это модель, в которой в качестве объясняющих переменных используются случайные ошибки в предыдущих временных периодах.
(6.5)
4. Авторегрессионная модель скользящей средней порядков pи q (ARMA(p,q)) – это модель, являющаяся объединением двух предыдущих, т.е. в ней в качестве объясняющих переменных используются как предыдущие значения ряда, так и предыдущие значения ошибок.
(6.6)
5. Авторегрессионная модель с распределенными лагами порядка pи q(ADL(p,q)) – модели, в которых учитываются лаги и в независимых, и в зависимых переменных:
(6.7)
Рассмотрим модели с лагами в независимых переменных (DL(p)). В том случае, если количество лагов конечно (например, для построения модели используются данные бухгалтерского баланса за 5 лет) модель может быть оценена при помощи обычного МНК для случая pнезависимых переменных.
Если же теоретически лагов может быть сколь угодно много (например, когда рассматривается фондовый рынок, на котором временные ряды для курсов акций могут быть построены с интервалом в 1 минуту), то для оценки неизвестных коэффициентов можно использовать два основных метода:
1. Метод последовательного увеличения количества лагов. Его применение осуществляется следующим образом.
1)
Рассматривается модель с одним
лагом: 
. Для нее вычисляются оценки и ошибки всех
коэффициентов.
2)
Количество лагов увеличивается на
единицу 
(до p) и
оцениваются параметры вновь построенной модели.
3) Если коэффициент (p–1)-й лаговой переменной изменил знак, то последняя лаговая переменная отбрасывается, и делается вывод о том, что следует рассматривать модель с p лагами. Иначе продолжаем.
4) Если коэффициент p-й лаговой переменной статистически незначим, то делается вывод о том, что следует рассматривать модель с p лагами. Иначе продолжаем.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.