2. Оценки коэффициентов, полученные по МНК, становятся очень чувствительными к изменениям исходных данных.
Рис. 4.2 Причины, последствия, методы обнаружения и устранения мультиколлинеарности
3. Затрудняется измерение вклада каждой из объясняющих переменных в объясняемую уравнением регрессии дисперсию зависимой переменной.
4. Возможно получение неверного знака у коэффициента перед объясняющей переменной.
В то же время при достаточно высоких значениях коэффициента детерминации в моделях, построенных для цели прогнозирования, мультиколлинеарность не является достаточно серьезной проблемой, и построенные модели вполне могут быть использованы на практике.
Проблема мультиколлинеарности обязательно должна быть решена в том случае, если целью модели является анализ характера влияния различных факторов на зависимую переменную.
Мультиколлиеарность можно определить при помощи следующих методов:
1. Анализ значений коэффициентов корреляции между объясняющими переменными. Высокие коэффициенты корреляции между объясняющими переменными
2. Сопоставление коэффициента детерминации и статистической значимости коэффициентов в модели. Коэффициент детерминации модели достаточно высок, но некоторые из коэффициентов в модели статистически незначимы.
3. Анализ вспомогательной регрессии – регрессии между объясняющими переменными. Для обнаружения регрессионной зависимости между объясняющими переменными строятся регрессионные модели типа:
, (4.14)
где j не равно i
для каждой объясняющей переменной.
Затем при помощи критерия Фишера (F-статистики) проверяется ее статистическая значимость:
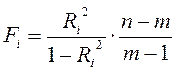(4.15)
Полученное значение сравнивается с критическим Fα; m-1; n-m. Если значение Fi оказывается больше критического, то делается вывод о том, что i-я независимая переменная является линейной комбинацией других и, следовательно, в модели присутствует мультиколлинеарность.
4. Анализ определителя матрицы корреляции независимых переменных.
Этот метод основан на том, что матрица, составленная из коэффициентов корреляции между объясняющими переменными, в случае отсутствия мультиколлинеарности имела бы определитель, равный единице (4. 11):
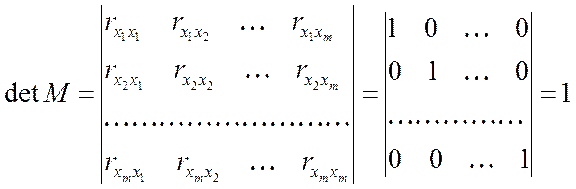(4.16)
При существовании мультиколлинеарности коэффициенты отличны от 0 (изменяются в пределах от –1 до 1), и определитель матрицы становится меньше. В случае совершенной мультиколлинеарности он равен 0:
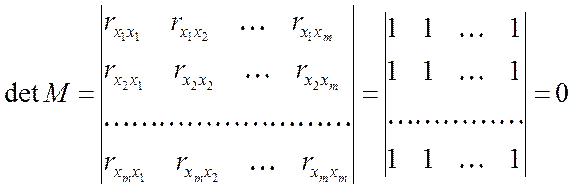(4.17)
Обнаружить мультиколлинеарность можно, проверив статистическую гипотезу по поводу равенства 1 определителя этой матрицы:
H0: det M = 1 (4.18)
Проверка осуществляется на основе критерия χ2(хи –квадрат). Доказано, что величина:
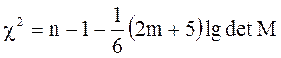(4.19)
имеет распределение χ2 с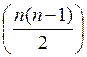 
степенями свободы.
Расчетное значение сравнивается с табличным (приложение 6), и если расчетное
значение оказывается больше, то считается, что мультиколлинеарность имеет
место.
Рассмотрим методы устранения мультиколлинеакрности.
1. Исключение коррелированных переменных из модели. Это наиболее простой способ борьбы с мультиколлинеарностью. Однако в этом случае возможны серьезные проблемы, связанные с тем, что полученные по упрощенной модели оценки будут смещенными.
2. Получение дополнительных данных или проведение нового наблюдения. Часто мультиколлинеарность проявляется вследствие неполноты данных, и при расширении выборки существенно уменьшается. Однако этот подход связан со значительными издержками, и, кроме того, может быть связан с появлением такого нежелательного явления, как автокорреляция.
3. Изменение спецификации модели. Может быть осуществлено как при помощи изменения аналитического выражения модели, так и путем добавления новых переменных, оказывающих существенное влияние на зависимую переменную. Этот метод целесообразно применять, если добавляемая переменная является «полезной», то есть существенно улучшает качество модели.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.