Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 43

Однако и в тесте Парка, и в тесте Глейзера не учитывается возможность появления гетероскедастичности в регрессиях (7.3) и (7.4). Если она будет иметь место, то вероятность обнаружения гетероскедастичности там, где ее в действительности нет, возрастет.

5.  Тест Голдфельда-Квандта. В этом тесте используется предположение, что дисперсия ошибок модели пропорциональна значениям независимой переменной. Исходная совокупность упорядочивается по мере возрастания значений независимой переменной, после чего исходная совокупность делится на 3 части размерами k, n-2k, k. Для первой и третьей подвыборок строят регрессионную модель, оценивают параметры и рассчитывают случайные отклонения. На основе этого определяется дисперсия случайных отклонений S²₁ и S²₃. Вывод о наличии гетероскедастичности делается в том случае, если различие между дисперсиями, определенное по критерию Фишера, оказывается статистически значимым. Формализовано тест Голдфельда-Квандта представим в виде следующего алгоритма (см. рис. 7.5)

Рис. 7.5 Алгоритм применения теста Голдфельда-Квандта

Рекомендуется выбирать значения k исходя из следующих соотношений:

Таблица 7.1

Рекомендуемые значения k для выборок различных размеров

При применении этого теста для анализа гетероскедастичности в моделях множественной регрессии рекомендуется проводить его для той независимой переменной, значения которой в наибольшей степени связаны с дисперсией случайных остатков. Если такую переменную невозможно выделить, то тест проводят для всех переменных. Важно учитывать, чтобы значения k были больше чем общее значение переменных (m+1).

Рассмотрите алгоритм применения теста Уайта

Для смягчения проблемы гетероскедастичности используют метод взвешенных наименьших квадратов (ВНК).

Основная идея метода состоит в том, что для смягчения проблемы гетероскедастичности следует «взвесить» наблюдаемые значения переменных с учетом соответствующей им дисперсии случайных отклонений (для этого используют среднеквадратическое отклонение ошибок: ).

В этом случае исходная модель преобразуется:

                                                          (7.5)

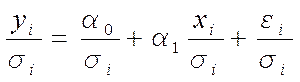                                                  (7.6)

введя замены: 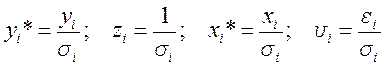 получаем модель, для которой выполняются предпосылки МНК:

                                                                (7.7)

Следовательно, рассчитанные по МНК оценки будут обладать свойством эффективности. Единственной проблемой, препятствующей реализации ВНК, является то, что обычно дисперсия случайных отклонений является величиной неизвестной.

Для преодоления этой проблемы используют два способа оценивания дисперсий: в первом случае предполагают, что они прямопропорциональны значениям независимой переменной, во втором – прямопропорциональны значениям квадратов независимых переменных.

Если предполагается, что дисперсии случайных отклонений прямопропорциональны значениям объясняющей переменной, то при анализе парной регрессии преобразованное уравнение регрессии (7.6) примет вид:

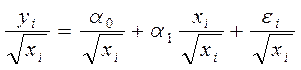                                                  (7.8)

Когда устраняется гетероседастичность в моделях множественной регрессии, обычно в качестве весов используют полученные теоретические значения зависимой переменной

                                                  (7.9)

и модель (7.6) имеет вид:

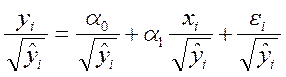                                                     (7.10)

Если же используется предположение о пропорциональности дисперсий ошибок квадратам значений индивидуальных переменных, то модель (7.6) будет иметь вид:

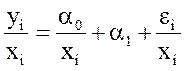                                                                     (7.11)

Следует отметить несколько общих положений, связанных с проблемой гетероскедастичности.

1.  Существуют ситуации, когда гетероскедастичность обусловлена влиянием переменной, не включенной в модель. В этом случае следует эту переменную отыскать и включить в анализируемую регрессию.