Экономика и менеджмент \ Эконометрика

Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 51

4.4.  Оценим доверительные интервалы для коэффициентов регрессии при разных уровнях значимости. Для этого воспользуемся формулами (3.33) и (3.34). Результат расчета занесем в таблицу:

Таблица 7

Доверительные интервалы для коэффициентов регрессии
при различных уровнях значимости

№п/п

Уровень значимости

Коэффициент

Доверительный интервал

1.

0,1

a0

(45,0;66,0)

2.

a1

(0,21;0,54)

3.

0,05

a0

(43,1;68,0)

4.

a1

(0,18;0,57)

5.

0,01

a0

(38,4;72,6)

6.

a1

(0,11;0,64)

4.5.  Рассчитаем доверительные интервалы для зависимой переменной. Для этого воспользуемся формулами (3.35) – для расчета доверительного интервала для среднего значения и (3.36) – для расчета доверительного интервала для индивидуальных значений. Результаты расчета для 5 %-го уровня значимости представлены в таблице и на графиках:

Таблица 8

Доверительные интервалы для зависимой переменной (уровень значимости – 5%)

№п/п

x

y

доверительный интервал

для среднего значения

для индивидуального значения

нижний предел

верхний предел

нижний предел

верхний предел

1

-75

35

27,3

4,06

50,61

-15,35

70,02

2

-18,9

46

48,4

33,80

63,02

9,76

87,06

3

0,1

65

55,5

43,10

67,99

17,66

93,43

4

9,6

65

59,1

47,47

70,76

21,48

96,74

5

31,2

74

67,2

56,43

78,02

29,85

104,60

6

36,3

49

69,1

58,33

79,96

31,76

106,52

7

39,8

58

70,5

59,58

81,34

33,06

107,86

8

49,5

49

74,1

62,82

85,38

36,58

111,62

9

53

81

75,4

63,93

86,90

37,83

113,00

10

68,7

98

81,3

68,47

94,15

43,29

119,33

11

162,4

124

116,5

89,32

143,69

71,57

161,45

сумм.

357

745

745

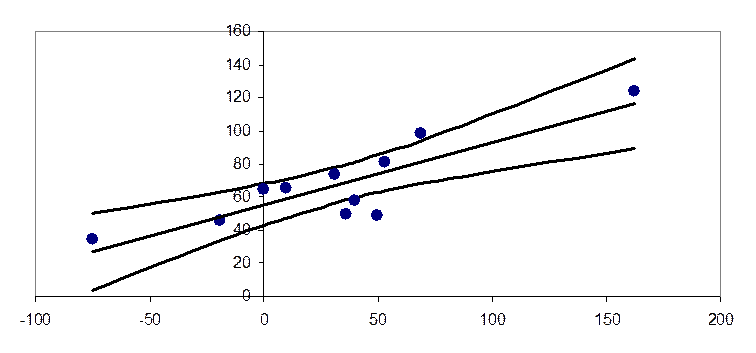
Рис. 3. Доверительные интервалы для среднего значения зависимой переменной. Уровень значимости – 5 %.

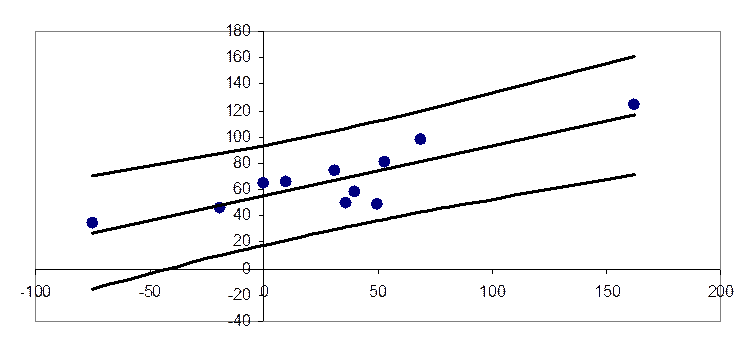
Рис. 4. Доверительные интервалы для индивидуального значения зависимой переменной. Уровень значимости – 5 %

5.  Коэффициент детерминации R2 достаточно высок (0,73), расчетное значение F-статистики для R2 (24,83) более чем в 4 раза больше критического (5,117), следовательно может использоваться на практике. В то же время существование необъясненной дисперсии предполагает возможность улучшить качество модели путем введения еще одной переменной.

6.  Как показал расчет, устойчивой связи между изменением сбережений и процентной ставкой нет. Оценим силу связи между приростными величинами: изменением сбережений и изменением процентной ставки (табл. 9):

Таблица 9

Расчет прироста процентных ставок

№п/п

месяц

Ставка по кредиту, %

Прирост ставки по кредиту, %

1

янв. 

17,9

 ---

2

февр.

15,9

-2,0

3

март

15,8

-0,1

4

апр.

18,3

2,5

5

май

17,7

-0,6

6

июнь

15,2

-2,5

7

июль

16,0

0,8

8

авг.

14,9

-1,1

9

сен.

13,4

-1,5

10

окт.

13,7

0,3

11

ноя.

14,7

1,0

12

дек.

15,0

0,3

сумма

170,6

-2,9

среднее

15,5

-0,3
Скачать файл