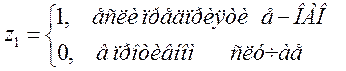 (5.1)
(5.1)
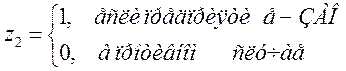 (5.2)
(5.2)
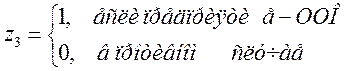 (5.3)
(5.3)
(предполагается, что круг рассматриваемых предприятий ограничивается только тремя организационно-правовыми формами: ОАО, ЗАО и ООО).
Как несложно заметить, число фиктивных переменных можно сократить, так как всегда будет выполняться равенство:
![]() (5.4)
(5.4)
В общем случае построенная с включением фиктивных переменных регрессионная модель может иметь вид:
а)![]() – модели, содержащие
только фиктивные объясняющие переменные, представляющие собой
кусочно-постоянные функции (они называются ANOVA – моделями или моделями
дисперсионного анализа)
– модели, содержащие
только фиктивные объясняющие переменные, представляющие собой
кусочно-постоянные функции (они называются ANOVA – моделями или моделями
дисперсионного анализа)
б) ![]() – модели, содержащие и
количественные, и фиктивные объясняющие переменные, и называемые ANCOVA– моделями или моделями ковариационного анализа). Такие модели имеют
вид множества функций, непрерывных на своей области определения. На практике чаще
рассматриваются модели ANCOVA, в которых фиктивные переменные играют уточняющую
роль.
– модели, содержащие и
количественные, и фиктивные объясняющие переменные, и называемые ANCOVA– моделями или моделями ковариационного анализа). Такие модели имеют
вид множества функций, непрерывных на своей области определения. На практике чаще
рассматриваются модели ANCOVA, в которых фиктивные переменные играют уточняющую
роль.
Можно выделить три основных направления использования моделей с переменной структурой: моделирование сезонных колебаний, моделирование институциональных изменений и учет влияния на результативный признак качественных факторов (рис. 5.1).
Учет сезонных колебаний осуществляется путем добавления 3 (если имеются квартальные данные) или 11 (если информация представлена по месяцам) фиктивных переменных. Учет институциональных изменений осуществляется путем добавления переменной, характеризующей данные как «до» и «после» изменений. Например, если рассматривается хозяйственная деятельность предприятия, и необходимо учесть влияние смены директора на его эффективность, то в модель необходимо добавить переменную z, такую, что:
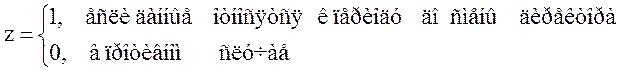
При применении модели в анализе качественных признаков (таких, как пол, социальный статус, форма собственности и т.п.) использование фиктивных переменных осуществляется по стандартной схеме.
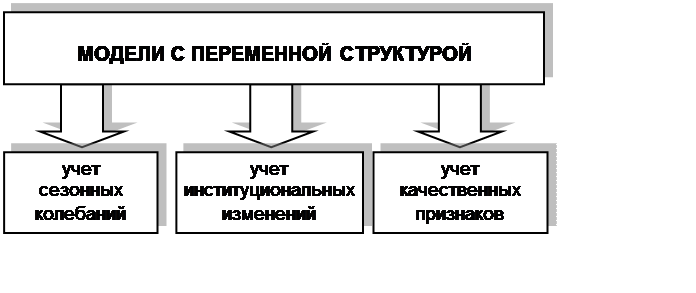
Рис. 5.1 Использование моделей с переменной структурой
Спецификация модели с переменной структурой обычно, в части фиктивных переменных, имеет вид линейной функции:
![]() (5.5)
(5.5)
Однако в ряде случаев возможно использование альтернативной фиктивной переменной (т.е. принимающей только два значения) в мультипликативной функции вида:
![]() (5.6)
(5.6)
Спецификация (5.6) используется, когда явно можно предположить, что изменение фиктивной переменной отразится не только на изменении начального уровня явления и параллельном сдвиге линии регрессии, но и на ее наклоне. Такое предположение возможно, в частности, когда рассматривается зависимость заработной платы от стажа и пола сотрудников, или же при учете институциональных изменений.
Последовательность решения задач эконометрического анализа моделей с переменной структурой после проведения спецификации модели не отличается от последовательности, применяемой в решении обычных задач множественной регрессии: это определение оценок неизвестных параметров при помощи МНК и оценка качества модели.
Обратите внимание, что для применения МНК необходимо выполнение его предпосылок, изложенных в теме 4.
Для определения оценок параметров в модели (5.5) можно сразу использовать МНК. Если же используется модель вида (5.6), то следует либо рассматривать несколько регрессий, в которых значения фиктивных переменных заданы, либо преобразовать переменные путем замены (в случае одной фиктивной переменной):
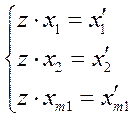 (5.7)
(5.7)
Тогда спецификация модели изменится, и она примет вид обычной множественной регрессии:
![]() (5.8)
(5.8)
Определение параметров в такой модели осуществляется при помощи обычного МНК, затем, в случае необходимости, можно вернуться к исходной форме.
Оценка качества моделей с переменной структурой осуществляется по тому же алгоритму, что и для обычной множественной регрессии.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.