Эконометрика: Учебно-методическое пособие (Изложение базовых знаний и основных практических навыков построения и использования эконометрических моделей), страница 35

Графические методы очень удобны, просты в применении, однако не позволяют точно установить, есть ли автокорреляция, в тех случаях, когда это не очевидно (рис. 6.8). Для них не существует однозначно определенного формального критерия, что сужает область их использования. Рекомендуется использовать графические методы для предварительной оценки наличия автокорреляции.

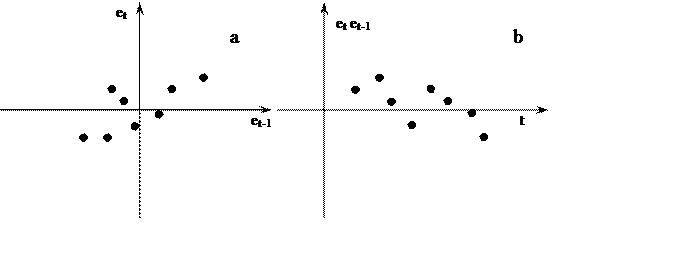
Рис. 6.8 Случаи, когда невозможно определить автокорреляцию при помощи графического метода

II.  Метод рядов. Этот метод позволяет точно определить, существует ли автокорреляция в исследуемом наборе данных. Алгоритм применения метода состоит из следующих этапов:

1.  Определяются знаки случайных отклонений, определяется количество рядов k – последовательности случайных отклонений с одним знаком. Для этого все случайные отклонения представляют в виде:

(– – – –)(+ + + + +)(– – – – – – – – –)(+ +)(– – –)

2.  Рассчитывают критические значения для k (k_low и k_high), исходя из предположения, что если автокорреляции нет, то kимеет нормальное распределение с математическим ожиданием M(k) и дисперсией D(k):

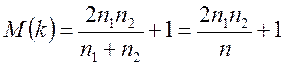                                                (6.14)

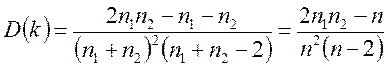                              (6.15)

где: n – объем выборки

n₁– общее количество единиц с положительным знаком случайного отклонения (количество знаков «+» в ряду)

n₂– общее количество единиц с отрицательным знаком случайного отклонения (количество знаков «–» в ряду)

Для заданного уровня значимости α критические значения будут равны:

                                                      (6.16)

                                                     (6.17)

Сравнивается фактическое значение количества рядов k с критическими значениями k_low и k_high . Если k ≤ k_low, то делается вывод о наличии положительной автокорреляции остатков. Если k ≥ k_high, то считается, что присутствует отрицательная автокорреляция. Если же k_low < k < k_high, то утверждается отсутствие автокорреляции.

Для небольшого числа наблюдений существуют специальные статистические таблицы k_low и k_high, разработанные Сведом и Эйзенхартом (см. приложение 5), при помощи которых упрощается процедура анализа автокорреляции.

III.  Критерий Дарбина-Уотсона (DW)

Суть метода в анализе статистики Дарбина-Уотсона, рассчитываемой по формуле:

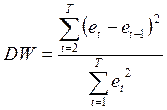                                                                   (6.18)

Доказано, что статистика Дарбина-Уотсона связана с коэффициентом корреляции между соседними отклонениями по формуле:

                                                              (6.19)

Следовательно, статистика DW принимает значения в интервале от 0 до 4. при этом можно сделать следующие выводы относительно значений DW (табл. 6.1)

Таблица 6.1

Значения, принимаемые критерием Дарбина-Уотсона и их интерпретация

Однако приведенной выше интерпретации статистики DW, как правило, недостаточно, чтобы сделать вывод о наличии либо отсутствии автокорреляции. Необходимо указать конкретные диапазоны DW, для которых характерно наличие или отсутствие автокорреляции. При грубой оценке предполагают, что автокорреляция не имеет место, когда 1,5 < DW < 2,5. Для точного определения наличия автокорреляции используются критические значения d_low и d_high из таблицы (приложение 4). Тогда интерпретация статистики DW примет вид:

Таблица 6.2

Интерпретация значений критерия Дарбина-Уотсона с использованием критических значений