Концепция формирования инновационной модели социально-экономического развития Харьковской области "Харьков как инновационный порт", страница 60

В данной матрице в качестве стратегий А выступают мероприятия, предла­гае­мые различными заинтересованными группами или подразделениями пред­приятия и направленные на достижение их целей. В качестве стратегий В пред­став­лены различные сценарии развития внешней среды с учетом периода времени. В качестве элементов матрицы a_ij выступает цель реализации того или иного мероприятия — прибыль, которая определяется как разница между резуль­татом и ресурсами, необходимыми для реализации мероприятия. Подобная модель позволяет реализовать сценарный подход к планированию.

В рамках предлагаемого подхода задачу согласования стратегического и оперативного направлений развития предприятия предлагается решить при исполь­зовании теории игр. При этом задача согласования должна описываться игровой моделью m ´ n и учитывать такие объекты согласования, как цели, мероприятия и ресурсы. Задачу согласования в рамках теории игр предлагается сформулировать следующим образом: каждой из заинтересованных групп предлагается реализовать определенное направление деятельности предприя­тия (А₁, А₂, …, A_i, …, А_m), что не противоречит общей цели предприятия. В качест­ве направлений деятельности могут выступать мероприятия, направленные как на раз­витие текущей позиции предприятия, так и на формирование стратегической позиции.

При реализации каждого из направлений деятельности получается целевой размер прибыли, который определяется с учетом ресурсов на реализацию пред­лагаемых мероприятий. Размер прибыли зависит от влияния факторов внеш­ней среды, которая может находиться в определенных состояниях (В₁, В₂, …, B_j, …, В_n) при условии ее изменения в различных временных интервалах (в кратко-, средне- и долгосрочном — степень нестабильности внешней среды может изменяться). Кроме этого, учет временного фактора необходим при определении прибыли от реализа­ции какого-либо мероприятия. Платёжная матрица Р задана элементами а_ij, харак­теризующими прибыль, которая получится при реализации i-го направ­ле­ния деятельности при j‑м состоянии внешней среды в определенный период времени:

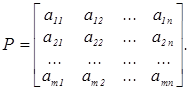
Целью задачи является или выбор такого направления деятельности, или их сочетания, реализация которых позволит получить величину прибыли, обеспечи­вающую достижение глобальной цели предприятия — выживание в долгосрочной перспективе с учетом состояния внешней среды и временного интервала полу­чения прибыли. Выигрыш, соответствующий оптимальному решению, называется ценой игры n. Если a= b= n, то игра называется игрой с седловой точкой. В этом случае выбор оптимального направления деятельности предприятия при опре­деленном состоянии внешней среды сводится к отысканию седловой точки. Если игра не имеет седловой точки, то применение чистых стратегий не дает опти­маль­ного решения игры. Оптимальное решение получается при чередовании случай­ным образом чистых стратегий. Применение чистых стратегий А₁, А₂, …, A_i, …, А_m с вероятностями p₁, p₂, …, p_i, …, p_m, причем сумма вероятностей равна 1 , называется смешанной стратегией S_A. Смешанные стратегии записываются в виде матрицы 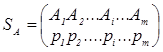 или в виде строки S_A= ( p₁, p₂, …, p_i, …, p_m). Ана­логично смешанные стратегии S_В обозначаются: 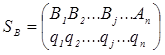 или S_В = (q₁, q₂, …, q_j, …, q_n), где сумма вероятностей стратегий равна 1 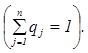 На основании принципа минимакса определяется оптимальное решение игры это пара смешанных стратегий S^*_A = ( p^*₁, p^*₂,…, p^*_m), S^*_B = (q^*₁, q^*₂, …q^*_n), элемен­ты которых означают вероятность применения соответствующих чистых страте­гий А_i, В_j, которая обладает следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то другому может быть выгодно отступать от своей. Обозначив x_i = p_i/n, i =1,2,…, m и y_j = q_i/n, j = 1,2,…, n, составляются две взаимно-двойственные задачи линейного программирования: