Этап 2. Представим поезд в виде одного тела весом (P+Q), на которое действуют продольные силы F и W (рис 5.1, в). Однако, на этом этане обращаем внимание на то что помимо поступательного движения часть массы поезда (колесные пары, якори тяговых электродвигателей локомотива) совершают вращательное движение, на что затрачивается часть движущей силы F.
Этап 3. Исключим из рассмотрения вращающиеся массы, условно увеличивая вес (массу) движущегося поезда умножением его на (1 + g). где g — коэффициент (доля) вращающихся масс в общей массе поезда. В результате получили одно движущееся поступательно тело (рис. 5.1,г). Его размеры не имеют значения для анализа, поэтому поезд можно считать материальной точкой (типовая модель механики), то есть точкой, в которой сосредоточена его масса и к которой приложены действующие силы.
Математической моделью поступательного движения такого поезда будет уравнение второго закона Ньютона, в котором действующая сила равна F - W, а масса тела (Р +Q)(1 +g)/q
Тогда 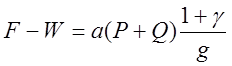 ,
,
где а — ускорение поезда; а = dv/dt.
Следовательно, 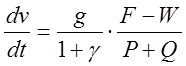 .
.
Обозначая через f и w величины удельных сил, получаемых делением сил F и W соответственно на вес поезда (Р + Q), получим окончательно в общем виде уравнение движения поезда:
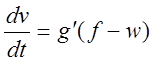 ,
,
где g'=g/(1 + g).
Вот так просто и выглядит основное уравнение математической модели поезда, принятой в тяговых расчетах. При этом надо иметь в и иду, что величины f и w в этом уравнении — переменные. Они, во-первых, сами зависят от скорости г> и, во-вторых, значения этих величин определяются конкретными конструктивными особенностями единиц подвижного состава, степенью загрузки вагонов и т. д.
Кроме того, в величину т вводятся в случае необходимости величины сил дополнительного сопротивления (от уклона профиля, кривизны пути и т. п.). Таким образом, внешне простая модель в действительности проработана достаточно детально. Поэтому она и служит давно и надежно для тяговых расчетов на железнодорожном транспорте с приемлемой для инженерных целей точностью.
Методы подобия и анализа размерностей в теоретическом исследовании. Вопросы соотношения параметров модели и объекта, то есть вопросы подобия модели и объекта, имеют важное значение в процессе моделирования.
Количественное соответствие между отдельными сторонами процессов, протекающих в реальном объекте и в его модели, характеризуется масштабами.
Подобие процессов в целом характеризуется критериями подобия. Критерий подобия процесса — это безразмерный комплекс параметров, характеризующих данный процесс. В науке используется целый ряд критериев подобия для различных физических процессов. В гидравлике — это критерий Рейнольдса, характеризующий режим течения жидкости; в теплотехнике — критерий Нуссельта, характеризующий условия теплоотдачи, и Кирпичева — для теплопередачи; в механике — критерий Ньютона и т. д.
Равенство значений этих критериев для модели и объекта обеспечивает подобие изучаемых процессов. Использование методов теории подобия позволяет выражать в обобщенной форме характеристики или описания однородных процессов, что дает возможность распространять результаты отдельных единичных опытов на классы подобных им процессов.
Подобие физических явлений, элементы теории подобия, моделирования на основе подобия недостаточно освещаются в учебных курсах общетехнических и специальных дисциплин, однако овладение ими необходимо инженеру-конструктору, проектировщику и исследователю. Для этого необходимо пользоваться специальной литературой по этим вопросам, например [2].
К теории подобия примыкает еще один метод научного теоретического исследования — метод анализа размерностей, который, к сожалению, в вузе не изучается даже в объеме понятия.
Опыт показывает, что физические закономерности выражаются только произведениями степеней физических величин (при этом, естественно, степени могут быть положительными и отрицательными, целыми и дробными). С другой стороны, размерности обеих частей равенства, выражающего физическую закономерность, должны быть одинаковы.
Эти два положения служат не только для проверки правильности тех или иных рассуждений, но и для поиска новых закономерностей, выявления связей между факторами, участвующими в процессе.
СПИСОК ЛИТЕРАТУРЫ
1. Диксон Дж. Проектирование систем: Изобретательство, анализ и принятие решений/Пер. с англ.—-М,: Мир, 4669—440 с.
Эта книга, как явствует та ее подзаголовка, имеет очень .широкое содержание Она охватывает все этапы работы инженера по проектированию и по содержанию была бы полезна при изучении тем гл. 1 и 4 настоящего пособия Но особенно -надо 'ее рекомендовать при изучении денной главы, вопросы инженерного анализа разработок в ней рассмотрены наиболее подробно.
2. Седов Л И Методы подобия я размерности -в механике 5-е изд. -М. Наука, 1965 —388 с.
Книга в целом посвящена анализу методами подобия и размерностей сложных физических процессов Но в первых двух ее главах рассмотрены общая теория размерности физических величин и принципы подобия, моделирования с примерами применения теории размерности
3 Математическое моделирование/Под ред. .Дж Эндртоса и Р Мак Лоуна Пер с англ.—М Мир, 1979—278с
В книге на примерах из различных отраслей науки и техники показы даются процессы построения их математических моделей, причем рассматривается, в первую очередь, не математическая, а методологическая сторона моделирования подход к описанию -и анализу реальной проблемы, сценка возможности ее идеализации, выбор пути построения модели, Степень ее пригодности и соответствия модели, методы проверки модели
4 Веников В. А., Путятин В. Введение в специальность Учеб пособие — М. Высш. шк., 1978 — 294 с
В последней главе книги популярно изложены принципы моделирования и подобия, приемы создания и применения моделей.
Глава 6
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.