На основе интуиции устанавливаются допущения, а здравый смысл помогает соблюсти равновесие между требованиями точности и полноты описания и усложнением и стоимостью решения. Уже первые исследования построенной модели показывают меру ее адекватности реальному процессу (по имеющимся данным) и устанавливают требования к ее дальнейшему совершенствованию (дополнению, уточнению зависимостей, допущений и т. п.).
Иногда используются другие подходы к построению моделей:
построение простейшей модели наиболее характерного для объекта процесса и последующее введение дополнений и поправок, учитывающих его особенности. Так, например, создаются модели элементов рабочего цикла двигателя внутреннего сгорания в его тепловом расчете — на основе моделей идеальных термодинамических процессов;
противоположный путь: создание сразу модели наибольшей возможной полноты (такие модели, например, создаются в задачах исследования операций). Такая модель носит обычно вероятностный характер и недоступна анализу без применения ЭВМ. Такое моделирование называют имитационным так как в модели имитируются и случайные факторы.
Проверка адекватности модели. Адекватность модели — это ее соответствие тому реальному физическому процессу (или объекту), который она представляет.
Проверка модели начинается и проходит в самом процессе ее построения, когда выбираются или устанавливаются те или иные взаимосвязи между ее параметрами, оцениваются принятые допущения. Однако после сформирования модели в целом надо проанализировать ее с некоторых общих позиций.
1. Математическая основа модели (то есть математическое описание физических взаимосвязей)должна быть непротиворечивой именно с точки зрения математики: функциональные зависимости должны иметь те же тенденции изменения, что и реальные процессы; уравнения должны иметь область существования не менее диапазона, в котором проводится исследование; в них не должно быть особых точек или разрывов, если их нет в реальном процессе, и т. д. Уравнения не должны искажать логику реального процесса. Типичная ошибка многих вполне добросовестных исследователей состоит часто в том, что используя известные физические законы, он и получают уравнения, в которых меняются местами функции и независимые переменные и которые потом используются как, объективные, первичные без специального доказательства. С точки зрения математики, если у = f(x), то можно считать что х = φ(у). С точки зрения физики, когда под символами " и х подразумеваются конкретные физические величины, в конкретных условиях это не всегда справедливо
Наглядный пример По закону Ома сила тока в цепи I прямо пропорциональна напряжению U и обратно - сопротивлению R, то есть I=U/R. Это выражение справедливо всегда, но, когда используется обратная формула U=I·R, ее некритическое применение может привести к ошибкам Нельзя сказать, например, что напряжение в электрической сети пропорционально произведению I•R, так как U в дан ном случае не функция, а параметр, зависящий от источника электроэнергии. В данном случае это очевидно, но во многих других ситуациях подобные инверсии не замечаются автора ми, что может приводить к неверным выводам.
2. Модель должна адекватно, то есть по возможности точно, отражать действительность. Адекватность нужна не вообще, а в рассматриваемом диапазоне. Точность модели не может превысить точности исходных данных и это нельзя упускать из виду, особенно в нашей железнодорожной практике, когда многие физические параметры вообще не имеют детерминированных значений. Надо помнить, что чем проще модель, тем удобнее ею пользоваться. В пользу простои модели говорят и следующие соображения.
если упрощенная модель даст приемлемые для целей исследования результаты, то есть окажется для них достаточно точной, то отпадает необходимость в лишней работе;
значительно легче вносить те или иные усложнения (за счет отмены части допущений) в уже разработанную модель, даже если она недостаточно точна, чем пытаться решать сразу сложную систему, еще не прочувствовав ее поведение в простой ситуации.
Расхождения между результатами анализа модели и реальным поведением объекта неизбежны, так как модель — это отражение, а не сам объект. С одной стороны, не надо затушевывать эти расхождения, как это пытаются делать неопытные исследователи, следует им дать реальную оценку, исходя из целей исследования. С другой - не следует слишком обольщаться своей удачей, если вдруг обнаружится, как пишут обычно, «практически полное совпадение» расчетов по модели с результатами эксперимента. Здесь всегда надо помнить, что «даже плохая теория может хорошо согласовываться с экспериментом, если существуют не учитываемые в теории погашающие друг друга эффекты» [3* с 56]. Отсутствие расхождений такого типа при наличии в модели упрощают и , допущений должно послужить исследователю сигналом о нeобходимости более подробного анализа задачи.
Пример построения модели. В качестве примера рассмотрим модель движения поезда, принятую в практике тяговых расчетов.
Общее представление о движущемся поезде дает расчетная схема (рис.
5.1,а). На ней поезд показан как совокупность локомотива и группы вагонов,
связанных вместе упругими 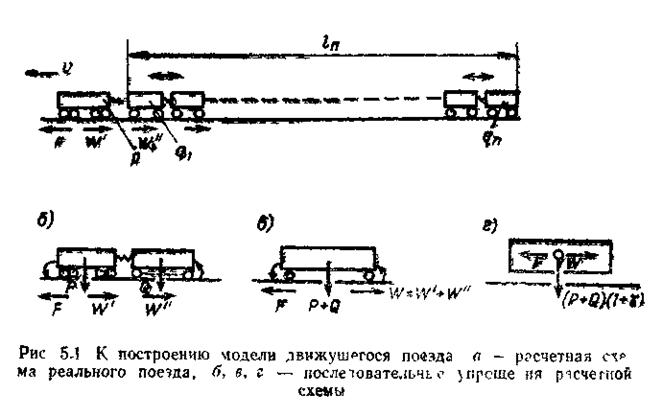
связями. На элементы поезда действуют силы тяги. сопротивления движению W, W, .... силы тяжести P,qi…, Поезд как совокупность единиц подвижного состава движется поступательно со, скоростью v. При этом подразумеваются- уже не которые допущения: не принимаются во внимание техническое состояние вагонов и локомотива, их вертикальные и поперечные колебания и т. д. Однако большое число объектов делает систему неприемлемой для анализа. Проделаем несколько последовательных упрощений
Этап 1. Объединим условно все вагоны состава и будем представлять их единым движущимся телом весом Q=Σq; и с общей силой сопротивления движению W". Наличием связей и возможностью относительных продольных перемещений вагонов пренебрегаем. Новая модель представляет собой два связанных тела (локомотив и состав), движущихся поступательно (рис. 5.1,6). Так как оба тела движутся с одной скоростью и в одном направлении, возможно дальнейшее упрощение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.