Подготовка данных для расчета параметров установившихся режимов и переходных процессов в электроэнергетических системах с помощью современных вычислительных комплексов: Учебное пособие, страница 38

r_э = кr_п   (м) - эквивалентный радиус,         r_п   (м) – радиус провода  жилы, к – коэффициент поверхностного эффекта, равный 0,779 для сплошных круглых жил,    

r_об = r_уд  = r_уд 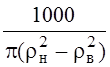 (Ом/км) – удельное активное сопротивление одного километра, как правило, свинцовой оболочки,    

r_уд = 0,252  (Ом×мм²)/м - удельное сопротивление  одного метра свинцовой оболочки сечением 1 мм²,  которое подставляется в формулу,  если наружный r_н и внутренний  r_в радиусы  оболочки заданы в мм,  если последние заданы в м,   то  r_уд = 0,252 ^. 10^-6  Ом×м,   если в см,  то  r_уд = 0,252 ^. 10^-20  ,

q = p ( r²_н - r²_в) –  сечение кабельной оболочки,  которое может быть задано в мм²,   м²,

l = 1000 м – длина одного километра кабеля в метрах,  если длина l  и радиусы r_н   и r_в  заданы в см, то  тогда   l = 100000 см, а r_уд = 0,252 Ом ^.см,

x_m @ x_об1 = 0,145 lg  (Ом/км) – практически равные друг другу удельные индуктивные сопротивления взаимосвязи оболочки с жилой и в целом оболочки при протекании по жилам токов прямой последовательности для одного километра кабельной линии.

Вид приведенного выражения индуктивного сопротивления прямой последовательности оболочки объясняется следующим:

1) индуктированные в оболочки токи прямой последовательности являются также токами прямой последовательности,

2) среднегеометрическое расстояние между оболочками D_сроб  жил благодаря конструкции рис.14 равно среднегеометрическому расстоянию между жилами D_ср,  т.е.  D_{ср об}  =  D_ср,

3) коэффициент поверхностного  эффекта равен практически единице, т.к. никакого поверхностного вытеснения протекающего тока не происходит. Это имеет место потому,  что оболочка в отличие от жилы имеет сечение тонкого кольца.  Поэтому вихревые токи контуров,  образующихся в теле оболочки в продольном ее направлении от кругового магнитного поля тока жилы и вызывающих эффект вытеснения за счет того,  что направление вихревого тока во внутренней глубине проводника оболочки противоположно направлению тока жилы,  а на поверхности совпадает с током жилы,  не могут сильно развить свое действие. Поэтому эквивалентный радиус оболочки r_эоб в данных условиях может быть принят равным среднему радиусу кольца, т.е. .  Следовательно,  формула для индуктивного сопротивления прямой последовательности оболочки может быть такой

x_об1 = 0,145 lg  = 0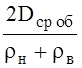,145 lg  = 0,145 lg .

Практически то же самое обоснование может быть представлено для  приведенного    выражения индуктивного сопротивления взаимосвязи оболочки с жилой. Действительно,  сопротивление  взаимоиндукции между оболочкой и жилой отдельного одножильного кабеля ничем не отличается от сопротивления самоиндукции фазы, так как определяется  одним и тем же  магнитным потоком между аксиальными оболочкой и жилой. Благодаря двум другим одножильным кабелям и протеканию  по жилам токов прямой последовательности имеет место влияние  двух других жил через их оболочки на самоиндукцию третьей оболочки, а, следовательно, и взаимоиндукцию последней оболочки с ее жилой, т.е. точно так же как это было при определении индуктивного сопротивления оболочки.  Поэтому

x_m = 0,145 lg  - 0,145 lg  = 0,145 lg , где D_з – средняя глубина протекания обратного тока в земле в м.

Первое положительное слагаемое выражения взаимоиндукции x_m моделирует составляющую за счет двух соседних жил в симметричном режиме (суммарный ток соседних жил имеет противоположное направление относительно тока в рассматриваемой жиле,  и он индуктирует в оболочке последней ток,  совпадающий с направлением тока в рассматриваемой жиле,  благодаря чему первая составляющая x_m  положительна и определяется как сопротивление самоиндукции),  а второе отрицательное слагаемое моделирует составляющую за счет тока,  индуктированного в оболочке током рассматриваемой жилы (индуктированный ток всегда противоположен по полярности индуктирующему, вследствие чего вторая составляющая x_m  отрицательна).