Подготовка данных для расчета параметров установившихся режимов и переходных процессов в электроэнергетических системах с помощью современных вычислительных комплексов: Учебное пособие, страница 37

Из рисунка видно, что формально межфазные емкости кабельной линии    могут быть определены выражениями:

С_АВ=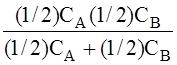,   С_АС=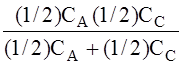,    С_ВС = 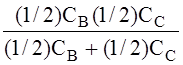    через половинные емкости,  а емкости фаз - суммами половинных емкостей:

С_A  =,   С_B  =,   С_C  = .

Так как С_А  = С_В  = С _С =С_о= С₁,  то  С_АВ = С_АС  = С_ВС  = (1/4)С_о=(1/4)С₁.   Те же самые соотношения имеют место и для поперечных активных проводимостей трехфазной линии из одножильных кабелей,  т.е. 

g_А= g_В = g _С =g_о= g₁,     g_АВ = g_АС  = g_ВС  = 1/4g_о=1/4g₁.

Таким образом, поперечные емкости и активные проводимости линии из одножильных кабелей  одинаковы для всех последовательностей, т.е.        С₁=С₂= С_о,     g₁ = g₂ = g_o  и собственные емкости проводимости также не отличаются от них. При   этом в уравнениях токов через поперечные емкости и активные проводимости исключаются составляющие типа                            С_АВ (- ),   g _АВ(U_А –U_В),   т.к.  межфазных емкостей типа С_АВ и проводимостей типа g _АВ фактически нет.

Для случаев  трехжильных кабелей, заключенных в общую оболочку, удельные продольные и поперечные параметры   радикальных отличий от параметров воздушных линий не имеют.

При составлении  матриц-стереотипов для систем жил и оболочек кабелей,  на основании которых формируются системы уравнений падений напряжений нулевой последовательности на продольных сопротивлениях  и системы уравнений токов нулевой последовательности через поперечные проводимости,  принципиальных отличий нет от аналогичных процедур для воздушных линий. То обстоятельство, что заземленные оболочки кабелей охватывают жилы кабеля, никакого заметного влияния на глубину протекания обратного тока не оказывает. Собственные и взаимные зеркальные изображения жил при этом,  как показывает анализ,  в расчетном смысле также не имеют никакого отличия от аналогичных изображений фаз воздушных линий. Также возможно укорочение по методу Гаусса систем уравнений жил и оболочек на количество уравнений оболочек и определение параметров жил с учетом оболочек,  но без самих оболочек.  Инвариантно это можно выполнить для непрерывно заземленных проводящих оболочек, т.е.  кабелей проложенных в земле, т. к. суммарные падения напряжений на продольных сопротивлениях оболочек, благодаря непрерывному их заземлению оказываются равными нулю. Аналогично суммарные  токи смещения и утечки между непрерывно заземленными оболочками и жилой также при этом всегда равны нулю,  т.к.  заряды оболочек относительно земли  равны нулю.  При таких условиях расширение матриц уравнений падений напряжений на продольных сопротивлениях,  токов смещения и утечки оболочек можно представить нулями.

В случае  гарантированного заземления оболочек в начале и конце кабельных  линий (кабели проложены в туннелях) процедура Гаусса по ликвидации уравнений оболочек будет как бы вариантной, так как будет зависеть от падения напряжения при протекании тока на всей длине оболочки от начала до конца кабельной линии. Однако принципиально инвариантность имеет место и в этом случае,  т.к.,  строго говоря,  падение напряжения  на оболочке пропорционально протекающим токам по ним. Следовательно, сопротивления  как отношения падений напряжений на них к току через них не зависит от падений напряжений.     Данную возможность,  к сожалению,  практически трудно реализовать,  так как необходимо точно знать значения расширений матрицы сокращаемых строк.

Ниже даны основные выражения для определения параметров кабельных линий,  выполненных одножильными и трехжильными кабелями.

Кабельная  линия выполнена тремя одножильными кабелями (рис.14)

Удельное сопротивление  (Ом/км)   прямой (обратной) последовательности

z₁ = z₂ = r₁ + jx₁ = r +Δr_{1 +} j( x – Δx₁) =r_п + + j (0,145lg 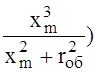 -,    где r₁ = r_п  – активное сопротивление прямой последовательности, равное собственному сопротивлению провода (жилы)  кабеля,

D_ср = == D  (м) -среднегеометрическое расстояние между жилами и оболочками,