Подготовка данных для расчета параметров установившихся режимов и переходных процессов в электроэнергетических системах с помощью современных вычислительных комплексов: Учебное пособие, страница 20

2.4.2.3  Трехобмоточный трансформатор (автотрансформатор)

Имеют место три межобмоточных сопротивления   z₁₂,  z₁₃, z₂₃ . Хотя  в

данном случае минимальная лучевая схема формально может содержать кроме трех лучей z₁,  z₂,  z₃  также  треугольник s₁₂,  s₂₃,  s₃₁. Однако может быть составлено только три равенства, так как заданы только три межобмоточных сопротивления  z₁₂,  z₁₃ и z_23,   в то время как  число неизвестных 6:  z₁,  z₂,  z₃,  s₁₂,  s₂₃,  s₃₁.    Данная противоречивость устраняется тем,  что треугольник сопротивлений s₁₂,  s₂₃,  s₃₁  исключается. При этом полнота и достоверность равенств не нарушаются,  а приходят в  соответствие с возможной  при имеющихся данных лучевой схемой замещения в виде звезды, т.е. без треугольника дополнительных сопротивлений. Нет основания для треугольника дополнительных сопротивлений также по чисто формальным признакам: 1) исходный (заданный) треугольник межобмоточных сопротивлений как минимальный из многоугольников не содержит диагоналей  или его диагонали  и стороны совпадают (вырожденный случай), поэтому совпадают межобмоточные сопротивления для граней и диагоналей, 2) преобразование исходного треугольника в треугольник и лучи схемы замещения лишено  всякого смысла,  т.к. не использует никакой дополнительной информации.

Следовательно схемой замещения трехобмоточного трансформатора (автотрансформатора) может  только звезда  (рис.6), сопротивления которой z_1, z₂ ,z₃   определяются из равенств-уравнений:

z₁₂  = z₁  + z₂ ,       z₂₃  =  z₂ + z₃,       z₁₃   =  z₁ + z₃, решение которых  дает известные  соотношения:

z₁  = 0,5 (z₁₂  + z₁₃ – z₂₃ ),    z₂  = 0,5 (z₁₂  + z₂₃ – z₁₃ ),    z₃  = 0,5 (z₂₃  + z₁₃ – z₁₂ ).

Вследствие малости активных составляющих  сопротивлений в практических расчетах полагают заданные межобмоточные сопротивления равными чисто реактивным сопротивлениям и переписывают выражения для звезды схемы замещения в виде:

x₁  = 0,5 (x₁₂  + x₁₃ – x₂₃ ),    x₂  = 0,5 (x₁₂  + x₂₃ – x₁₃ ),    x₃  = 0,5 (x₂₃  + x₁₃ – x₁₂ ), где буквой  x  обозначены   индуктивные сопротивления лучевой схемы и исходного треугольника.

Расчеты обычно ведутся  в относительных  единицах, поэтому заданные межобмоточные сопротивления  равны напряжению КЗ, т.е.

U₁₂ = z₁₂  @ x₁₂,    U₁₃ = z₁₃  @ x₁₃,     U₂₃ = z₂₃  @ x_23..

Активные межобмоточные сопротивления и сопротивления  лучей определяются для трехобмоточных трансформаторов  и автотрансформаторов равенствами-уравнениями мощностей потерь КЗ,  аналогичными равенствам-уравнениям  сопротивлений или напряжений КЗ. Поэтому можно получить для трехобмоточных трансформаторов:

ΔN₁  = 0,5 (ΔN ₁₂  + ΔN ₁₃ – ΔN ₂₃ ),

ΔN₂  = 0,5 (ΔN ₁₂  + ΔN ₂₃ – ΔN ₂₃ ),

ΔN₃  = 0,5 (ΔN ₂₃  + ΔN ₁₃ – ΔN₁₂ ), для автотрансформаторов:

     ,                                                                

     ,                                                        

    ,                                                                  

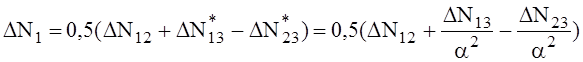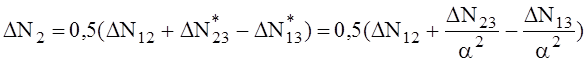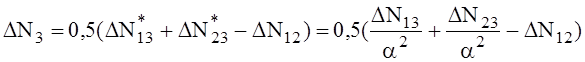где  буквосочетаниями ΔN обозначены  потери в активных сопротивлениях исходного межобмоточного треугольника (две цифры в нижних пределах) и принятой лучевой схемы в виде звезды (одна цифра  в нижних индексах);

a = S_т / S_ат  = S_нн / S_н   -  относительная доля габаритной мощности   S_т = S_нн обмотки низшего напряжения автотрансформатора относительно его номинальной (проходной) мощности  S_ат = S_н,

ΔN₁₃, ΔN₂₃ - межобмоточные активные потери мощности КЗ  автотрансформатора  предполагаются отнесенными  к его типовой или номинальной мощности третичной обмотки,  а потери ΔN ₁₂ - к номинальной (проходной) мощности автотрансформатора,

ΔN₁, ΔN₂, ΔN₃  - активные потери лучей (обмоток) при используемых формулах оказываются отнесенными к номинальной мощности  автотрансформатора.

Если потери ΔN₁₃, ΔN₂₃ были бы отнесены к номинальной (проходной) мощности,  т.е.  ,    ,  то  a  было бы  равно единице.  Это отражают левые части выражений потерь  ΔN₁,  ΔN₂,  ΔN₃.