Подготовка данных для расчета параметров установившихся режимов и переходных процессов в электроэнергетических системах с помощью современных вычислительных комплексов: Учебное пособие, страница 28

Активное сопротивление r_з фазы обусловлено тремя составляющими:  собственной и внесенными двумя другими фазами благодаря взаимодействию по токам нулевой моследовательности с рассматриваемой фазой.  Анализ показывает,  что все составляющие равны между собой для линии с симметричными схемными параметрами (например, симметрированных путем транспонирования линий).  Для индуктивно    взаимосвязанных линий по нулевой последовательности протекание токов нулевой последовательности в фазах других линий привносит дополнительные составляющие взаимодействия в сопротивление нулевой последовательности каждой фазы рассматриваемой линии,  как реактивные,  так и активные.  Последние по величине от каждой фазы взаимодействующих с рассматриваемой линий привносят в фазу рассматриваемой линии удельное активное сопротивление 0,05 Ом/км,  а от трех фаз - соответственно 0,15  Ом/км.

Приведенные одинаковые приближенные значения по удельному сопротивлению нулевой последовательности фазы:  собственному и от взаимодействия с другими фазами рассматриваемой линии,  фазами других линий могут быть уточнены с учетом частоты f,  удельной проводимости земли l, среднегеометрических расстояний до фиктивных проводов возврата токов нулевой последовательности в земле на эквивалентной глубине D_з: собственного  и от других фаз ,  угла q между вертикалью,  проходящей через фазу,  и направлением на фиктивные провода возврата токов нулевой последовательности других фаз в земле на эквивалнтной глубине D_з.  С этой целью выполняются расчеты по формулам:

-для собственной составляющей фазы:

,

;

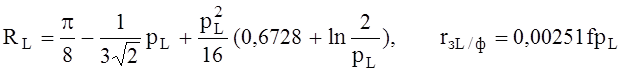-для составляющих взаимодействия с другими фазами рассматриваемой линии и фазами других линий

,

,

.

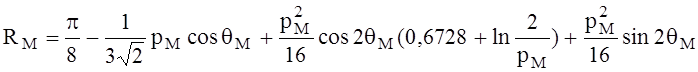В схему замещения нулевой последовательности каждой фазы сопротивление r_з  вносится как сопротивление взаимодействия с тремя фазами собственной линии,  т.е. ,  и любой другой линии,  т.е. .

Удельная емкость  и емкостная проводимость нулевой последовательности на землю могут быть рассчитаны точно по формулам:

С_о =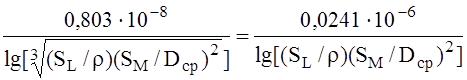 (Ф/км),  b_о=2pfC_о ( См/км), однако для практических целей часто вполне достаточным является использование имеющих место приближенных  соотношений между параметрами прямой и нулевой последовательностей:

при неучете или изолированных тросах   С_о @ (0,55-0,6)С₁,   b_о  = (0,55-0,6)b₁, при наличии тросов     С_о @ (0,65-0,7)С₁,        b_о  = (0,65-0,7)b₁.

Сопротивления прямой и нулевой последовательностей могут быть сформированы через собственное сопротивление фазы z и сопротивление межфазного взаимодействия  z_мф.  Анализ [3] дает следующие соотношения:

z₁ = z - z_мф,                z_о = z +2z_мф  ,    откуда следует:  z_мф  =,   z =  z₁+z_мф,    z = z_о - 2z_мф,  z_о = z₁ +3z_мф.

Такие же соотношения имеют место также для активных и реактивных составляющих сопротивлений,   в том числе индуктивностей.

Анализ показывает, что поперечные проводимости прямой y₁  и  нулевой у_о  последовательностей, также межфазная проводимость у_мф для симметричной трехфазной линии имеют взаимосвязь,  дуальную взаимосвязи продольных сопротивлений,  т.е.

у₁ = у_о + 3 у_мф,    у_мф = ,   у_о = у₁- 3 у_мф.

Однако собственная проводимость у связана,  например,  с проводимостью нулевой последовательности не через межфазную проводимость у_мф   как следовала бы ожидать на основании приведенных  соотношений,  а через проводимость взаимосвязи у_вз по формуле  у = у_о +  у_вз,   причем у_вз   может отличаться от у_мф  весьма заметно, например в 1,5 раза.  При этом понятие собственной проводимости у оказывается введенным  как бы формально.     Так получается потому,  что естественные соотношения имеют место не для поперечных проводимостей, а для соответствующих им поперечных сопротивлений.

Аналогичная картина  имеет место для активных составляющих и емкостей поперечной проводимости:

g₁ = g_о + 3g_мф,         g_мф = ,     g_о = g₁ - 3g_мф,           g = g_o + 3g_вз,

С₁ = С_о + 3С_мф,      С_мф = ,      С_о = С₁ - 3 С_мф,       С = С_о + С_вз.