Подготовка данных для расчета параметров установившихся режимов и переходных процессов в электроэнергетических системах с помощью современных вычислительных комплексов: Учебное пособие, страница 33

c_взta = c_взtb = c_взtc = c_взtsa = c_взtsb = c_взtsc = c_взтф,   c_взtts = c_взтт,   g_взta = g_взtb = g_взtc = g_взtsa = g_взtsb = g_взtsc = g_взтф,   g_взtts = g_взтт.

Примеры     матриц-стереотипов для индуктивностей самоиндукции            для активных сопротивлений:

и взаимодействия                           собственных и взаимодействия матрица  расширение  матрица расширение      ,              ,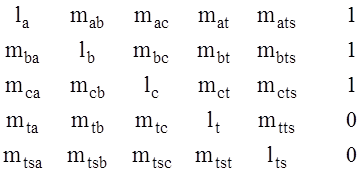

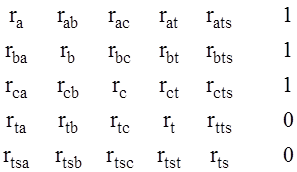для собственных емкостей и емкостей взаимодействия матрица                                            расширение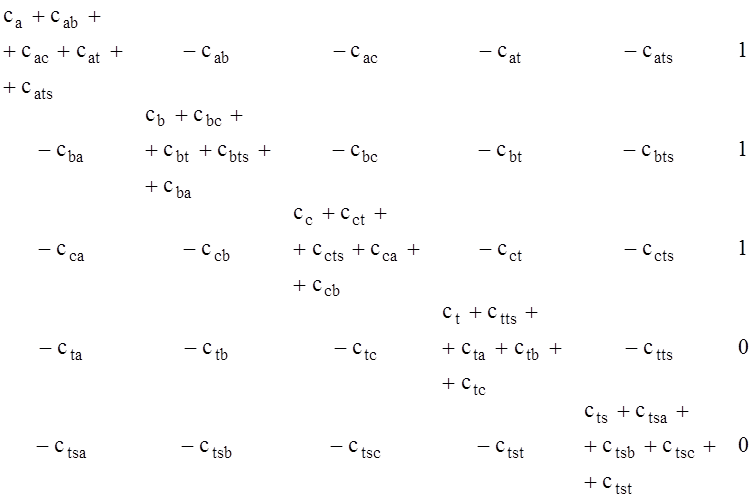

для собственных активных проводимостей и активных проводимостей взаимодействия матрица                                                 расширение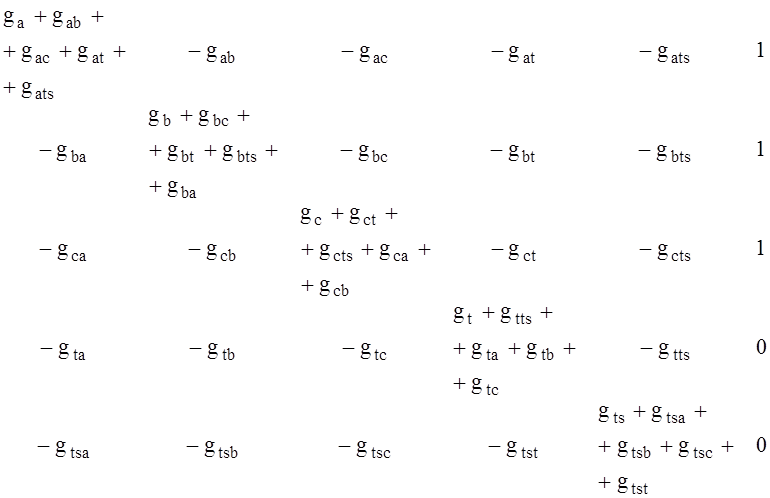  

Параметры прямой (обратной)  и нулевой последовательности формируются как результирующие при  действии симметричных электрических величин разных последовательностей во всех фазах [1]. В результате может быть получено  при отсутствии тросов:

l₁ = l – m,           l_o = l + 2m,        l_o = l₁ + 3m,            l = l₁ + m,

r₁ = r– r_мф,          r_o = r+ 2r_мф,       r_o = r₁ + 3r_мф,          r = r₁ + r_мф,

C₁ = C_o + 3C_мф,  C_o = C – C_вз ,    C_о = C₁ – 3C_мф ,      C = C_о+ C_вз,

g₁ = g_о + 3g_мф ,   g_о = g – g_вз ,      g_о = g₁ – 3g_мф ,        g = g_о +g_вз,

где индекс  1 относится к параметрам прямой,  а  о – к параметрам нулевой последовательности.

При наличии тросов  (одного или двух) необходимо составить соответствующие матрицы из индуктивных, емкостных и активных параметров с нулевыми расширениями для тросов и единичными для фаз, учтя  при этом имеющуюся симметрию параметров. Далее по процедуре Гаусса укоротить матрицы,  ликвидировать строки с параметрами тросов. Полученные результаты можно обработать по вышеприведенным формулам прямой и нулевой последовательности.

В заключение следует отметить следующее для практической работы с параметрами линий:

-  приведенные матрицы для индуктивностей и емкостей могут быть использованы для индуктивных  сопротивлений и емкостных проводимостей на частоте промышленного тока;

-  матрицы могут быть использованы как для удельных,  так и полных параметров всей линии;

- матрицы могут быть использованы также для эквивалентных радиусов фаз,  тросов,  межфазных,  межтросовых,  в целом межпроводных расстояний,  которые  все вместе составляют полную систему геометрических расстояний и которые могут быть укорочены на компоненты,  обусловленные тросами с целью расчета схемных параметров фаз с учетом влияния тросов, расстояний фаз и тросов до зеркальных отображений,  а также до зеркальных отображений  соседних фаз и тросов, которые необходимы для расчета емкостных параметров;

- матрицы могут быть расширены на любое количество фаз, тросов взаимодействующих линий;

- удельное активное сопротивление взаимодействия при частоте промышленного тока  f=50 Гц:  r = 0,000987f  0,05 (Ом/км);

-  удельная активная проводимость прямой последовательности  фазы линии относительно земли может быть оценена по формуле:

g₁ = 0, 093 ^. 0,05N_a /l_a /U²   (См/км), где N_a  (МВт) максимально передаваемая мощность по линии как  представителя класса напряжений U  (кВ), l_a  (км) – максимальная длина  линии как представителя класса напряжений U  и ориентировочно равна:

для линий  500 кВ  ~ 1,6 ^. 10 ^–8 См/км,  для линий 220 кВ ~ 8 ^.10^-8 См/км, для линий 110 кВ  ~ 1,6 ^. 10^-7 См/км, удельная активная проводимость между фазами линии ориентировочно равна:

для линии 500 кВ  ~ 1,3 ^.10^-9 См/км,  для линий 220 кВ ~ 0,8 ^.10^-8  См/км, для линий 110 кВ  ~ 1,35 ^.10^-8 См/км, удельная активная проводимость взаимодействия приближенно равна:

для линий 500 кВ ~ 2,5^. 10^-9 См/км,  для линий 220 кВ ~1,4 ^.10^-8  См/км, для линий 110 км ~ 2,3 ^.10^-8 См/км.

2.4.3.3  Системы взаимодействующих линий

Нескомпенсированные  (неуровновешанные) магнитные и электрические поля при несимметриях, обусловливающих  нулевую последовательность, требуют учета параметров схем замещения нулевой последовательности не только в пределах отдельных линий,  но также между взаимодействующими линиями или цепями (рис. 11).