Подготовка данных для расчета параметров установившихся режимов и переходных процессов в электроэнергетических системах с помощью современных вычислительных комплексов: Учебное пособие, страница 29

При этом имеют место следующие формулы через собственное удельное сопротивление утечки фазы R и удельное сопротивление взаимодействия токов нулевой последовательности R_вз=0,05 Ом/км,  удельные собственные a и взаимные a_вз   потенциальные коэффициенты,  а также удельные сопротивления прямой R₁ и нулевой R_o последовательностей утечки,  удельные потенциальные коэффициенты прямой a₁   и  нулевой a_о   последовательности:

g = 1/R,    C = 1/a,    g₁ = 1/R₁= 1/(R-R_вз),    С₁ = 1/a₁=1/(a-a_вз),

g_о = 1/R_o = 1/(R+3R_вз),     С_о = 1/a_o = 1/(a+3a_вз),

,    

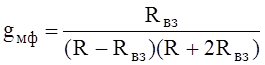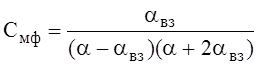
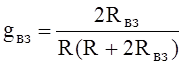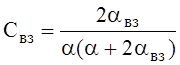,      , где   a = 41,4 ^.10⁶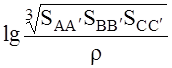 = 41,4 ^. 10⁶ lg ,

a_вз = 41,4 ^.10⁶ = 41,4 ^. 10⁶ lg .

Из формул видно,  что для потенциальных коэффициентов  имеют место те же соотношения,  что и для продольных сопротивлений,  т.е.

a₁= a_о  - a_вз,   a_о = a +2a_мф,   a_о = a₁ +3a_мф, a =  a₁+a_вз,   a_вз  =.

2.4.3.2  Влияние  грозозащитных тросов на параметры одиночной линии

Приведенные выражения  параметров одиночной линии представлены в предположении непроводящих грозозащитных тросов,  т.е.  изолированных от земли,  или полного отсутствия тросов.  Тогда непроводящие (многократно электрически разорванные) тросы не окажут влияния на индуктивное взаимодействие,  а  изолированные от земли  тросы не повлияют на электрическое взаимодействие фаз (на поперечные емкостные и активные проводимости линий). Современная практика построения воздушных высоковольтных линий такова, что тросы могут быть как непроводящими, так и проводящими,   но  они обязательно повторно заземлены либо на всех,  либо на части опор.  В связи с этим необходимо показать,  как изменяются параметры линии при заземленных и проводящих тросах.

За основу принимается система линейных уравнений для каждой фазы и троса линии.  Тогда,  как  показывает анализ,  можно  составить квадратную матрицу-стереотип из обозначений фаз, которая является основой системы линейных уравнений,  составленных по законам Кирхгоффа для участка взаимодействующих линий: системы падений напряжений на продольных сопротивлениях,  системы токов через поперечные проводимости участка линии в зависимости от того,  что будет подставлено вместо обозначений.  Квадратная матрица может быть расширена на столбец правой части уравнений, который представляет собой вектор суммарных падений напряжений на продольных сопротивлениях каждой фазы и троса или суммарный ток через поперечные проводимости.

Строки матрицы-стереотипа и их расширения формируются для каждой фазы и троса. Например, для одиночной линии, обладающей тремя фазами   a, b, c и двумя тросами t, t_s :

матрица-стереотип                           расширение

Для моделирования падений напряжений на участке линии от тока фазы или троса и токов соседних фаз и тросов в качестве элементов строк левой части матрицы подставляются произведения собственных и взаимных продольных параметров (индуктивностей и активных сопротивлений)  на  соответствующие производные и сами токи фаз и тросов,  а в правой части - суммарные падения напряжения на каждой фазе и тросе.  Например,

l_a + r_ai_a       m_ab + r_abi_b   m_ac+ r_aci_c    m_at + r_ati_t    m_ats +r _atsi_ts        ΔU_a ,

¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼

m_tsa+ r_tsai_a  m_tsb+ r_tsbi_b   m_tsc + r_tsci_c   m_tst+ r_tsti_t    l_tsts+ r_tstsi_ts         ΔU_ts , где буквой l обозначены коэффициенты самоиндукции  (собственные индуктивности,  одиночные индексы),  а буквой  m - коэффициенты взаимоиндукции (двойные индексы),  соответственно буквой r с одиночными индексами представлены собственные,  а с двойными индексами - взаимные   (вызванные протеканием токов соседних фаз по земле)  активные сопротивления фаз и тросов.

Если между составляющими левой части матрицы  проставить знаки  + (плюс),  а перед расширением каждой строки (правой частью) - знак  = (равенства),  то получится система линейных дифференциальных уравнений относительно токов фаз: i_a,  i_b,  i_c   и  тросов:  i_t,  i_ts.