Планирование и организация эксперимента, курс лекций, страница 49

Для исследования порядкового фактора первых двух воздействий А и В взаимодействие третьего порядка Х₁Х₂Х₃ (высшего порядка) приравниваем  к  фиктивному Хn. Оценка порядковых эффектов в таких планах осуществляется обычным образом, как и для эффектов варьируемых факторов. В одном случае, модель будет содержать эффекты варьируемых факторов и их взаимодействий, а также эффект порядка изменения факторов которые рассчитываются по обычным формулам для плана 2^к .

  ;         ;      

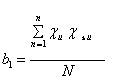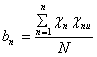
В случае всех порядково-зависимых факторов  в указанном плане, можно приравнять взаимодействие Х_1, Х₂ = Х_n2 (АС_, СА); Х_1, Х₃ = Х_n2 (ВС, СВ)

Анализ таких планов сводится к проверке значимости всех эффектов модели, включая порядковые, отбрасыванию тех из них, которые меньше своего интервала и проверке адекватности модели, содержаться только оставшиеся значимые модели. Аналогичный принцип построения плана для многоуровневых переменных с учётом порядка их испытаний позволяет строить соответствующие модели зависимости выходных показателей как от дозировок воздействий фактора, так и порядка их испытаний.

План МФИ для построения комбинированных моделей, учитывающих одновременно влияние дрейфа выходного показателя и порядковых эффектов факторов.

Для одновременного учёта дрейфа выходного показателя и порядковых эффектов многих факторов, можно также использовать обычные  факторные планы ПФЭ и ДФЭ в которых часть способов соответствует для представления дрейфа и не используется для варьирования факторами, а часть оставшихся столбцов соответствует порядковым (факторам, фиктивным). Примером такого плана может быть рассмотренный в разделе планирование в условиях дрейфа план, в котором первые к=3 столбца служат для представления линейного дрейфа выходного показателя У и не использования варьирования исследования факторов . Указанные факторы  варьируются согласно столбцам взаимодействия  ; ; , а порядковый эффект приравнивают уравнением  АВ и ВА.