Легко увидеть, что опыты плана 2 к представляют собой вершины квадрата, охватывающего интересующую область экспериментирования с центром в исходных (обычно лучших, известных до постановки эксперимента) условиях.
В случае к=3, точки плана
23=8 будут вершинами куба, определяющего область интересующих
режимов. По 8-ми точкам такого плана строится модель зависимости ![]() , по которой можно вычислить (у) при
любых (х) без постановки опытов, поскольку зависимость
, по которой можно вычислить (у) при
любых (х) без постановки опытов, поскольку зависимость ![]() ее
представляют в виде разложения в ряд Тейлора в точке соответствующей центру
эксперимента.
ее
представляют в виде разложения в ряд Тейлора в точке соответствующей центру
эксперимента.
Эта модель имеет вид многомерного полинома:
Для к=2:
![]() .
.
Где коэффициенты ![]() характеризуют силу влияния каждого
из факторов, а их знак - направление влияния факторов. То же относится и
коэффициентам
характеризуют силу влияния каждого
из факторов, а их знак - направление влияния факторов. То же относится и
коэффициентам ![]() , характеризующим силу и
направление влияния взаимодействия факторов.
, характеризующим силу и
направление влияния взаимодействия факторов.
Для к=3:
![]() .
.
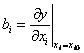 ;
; 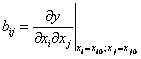 .
.
Благодаря оптимальным свойствам плана 2к все коэффициенты его полиномиальной модели оцениваются независимо друг от друга с одинаковыми минимальными дисперсиями (с максимальной точностью).
Расчет коэффициентов модели, ее анализ и интерпретация чрезвычайно просты и могут быть осуществлены без применения ЭВМ.
 Условие
оптимальности плана 2к:
Условие
оптимальности плана 2к:
1-Условие симметрии;
2-Условие нормирования;
3-Условие ортогональности.
Рассмотрим план 22//4. Полная расчетная матрица для оценки всех коэффициентов модели будет иметь следующий вид:
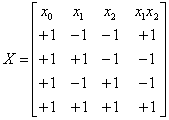
![]()
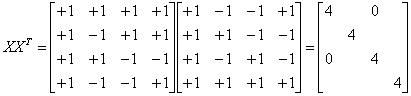
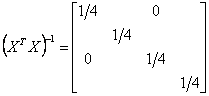
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.