Планирование и организация эксперимента, курс лекций, страница 23

Она характеризует сумму квадратов отклонений между экспериментально наблюдаемыми  и  значениями выхода в точках плана, поделенных на число степеней свободы .

; .

; ; .

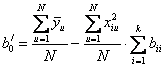Для нашего случая  = 79,11.

Для проверки адекватности полученной модели в нее подставляют значения переменных х в каждом опыте плана, и далее вычисляют дисперсию неадекватности  как сумму квадратов отклонений, экспериментально наблюдаемых и предсказываемых по модели  результатов.

 равно числу опытов плана N за вычетом числа значимых коэффициентов .

.

Поскольку расчетное значение F=3,6 оказалось меньше соответствующего критического значения из таблицы для уровня значимости 0,05 и числа степеней свободы числителя = 3 и знаменателя = 8, то есть F_табл = 4,07, то модель адекватно описывает результаты эксперимента.

Заключительный этап анализа сводится к каноническому преобразованию квадратичной модели с целью определения координат оптимума и исследования характера зависимости у от исследуемого фактора х в области оптимальных режимов.

Переход к канонической форме полученной адекватной модели сводится к ее записи в следующем стандартном виде:

, где:

Х_i – переменные канонической формы;