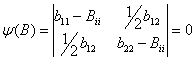
Тогда:
![]() .
.
В11 = -6,79; В22 = 13,49.
3. Уравнение в канонической форме имеет вид: У = 77,7-6,79х12+13,49х22.
Из этого видно, что исследуемая зависимость в оптимальной области имеет минимальный характер.
После получения канонической формы необходимо определить значение особой точки (ее координат) в физических переменных.
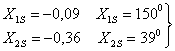 координаты
физических переменных.
координаты
физических переменных.
В случае большого числа
факторов получение коэффициентов канонической формы, то есть решение
характеристического уравнения порядка выше третьего, представляет значительную
вычислительную трудность. При этом может оказаться, что с точки зрения объема
вычислений, локализацию оптимального режима легче провести по исходной модели
методом “сеток”. Для этого в полученное уравнение подставляют значения исходных
переменных хi с шагом ![]() (хi +
(хi + ![]() ) и вычисляют значения
выходного показателя у в сетке узлов с координатами по каждой
переменной.
) и вычисляют значения
выходного показателя у в сетке узлов с координатами по каждой
переменной.
Второй семестр.
Планирование эксперимента в условиях неоднородностей типа дрейфа и порядковых эффектов факторов в задачах многофакторных испытаний.
Этап испытаний технических систем (машин, механизмов, технологического оборудования и его элементов) и материалов различного назначения является одним из важнейших этапов жизненного цикла в производстве подобной продукции, который определяет ее итоговое качество. Содержание и особенности современных задач многофакторных испытаний (М.Ф.И.) заключается в изучении одновременно комплекса переменных. Или могут быть режимные и конструктивные параметры исследуемых объектов технических систем, их элементов; состав и технология получения материалов; факторы условий их эксплуатации и состояния окружающей среды, влияющие на выходные показатели качества. В роли последних могут выступать эксплуатационные свойства испытываемых машин, их надежность и работоспособность, частота и характеристика отказов при функционировании, физико-механические характеристики прочности и износостойкости материалов и т.д.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.