Планирование и организация эксперимента, курс лекций, страница 35

Для проверки значимости, аналогичным образом, вычисляют доверительные интервалы для каждой группы коэффициентов модели умножением ошибки в определении этого коэффициента S{b_i^g} на значение t критерия Стьюдента, взятого из таблиц для уровня значимости  и числа степеней свободы f, с которым была определена ошибка воспроизводимости результатов эксперимента S_y².

Коэффициенты модели, которые по модулю превышают доверительный интервал  (|b_i ^g | > ) считаются статически значимыми и сохраняются в модели, а те коэффициенты, которые меньше, выбрасываются из модели как незначимые.

Заключительный этап анализа состоит в проверке адекватности полученной модели, включающей только значимые коэффициенты, с помощью F критерия Фишера. Для этого как обычно вычисляют дисперсию неадекватности S_ад по формуле:

S²_ад = ;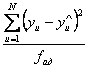

.

где:

      l – число значимых коэффициентов;

      у_u – экспериментально наблюдаемые значения;

      f_ад -  число степеней свободы;

      N – число опытов плана;

      - предсказываемая модель.

Если расчетное отношения дисперсии неадекватности к дисперсии воспроизводимости будет < соответствующего критического значения F критерия Фишера, взятого из таблиц для уровня значимости  и числа степеней свободы f_ад и f_y, то модель адекватно описывает результаты эксперимента.

F = 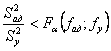; f_ад = ; f_y = .

где: m – число повторных наблюдений результата эксперимента.