Планирование и организация эксперимента, курс лекций, страница 34

y = b₀ +  + ;  y = b₀ +  + П + .

Для анализа результатов эксперимента по многоуровневому комбинаторному плану необходимо от матрицы плана эксперимента перейти к его расчетной матрице, состоящей из так называемых ортогональных контрастов (от Х к ) факторов. Если фактор имеет р_i уровней, то число ортогональных контрастов будет равно (р_i – 1).

В нашем случае, каждый из 4-х факторов имеет по три уровня (0, 1, 2), то есть каждому фактору соответствует два ортогональных контраста  и , и эти контрасты (ортогональные полиномы Чебышева) берут из таблиц целочисленных значений полиномов Чебышева.

Формулы для вычисления коэффициентов модели, представленной через полиномы Чебышева, получают методом наименьших квадратов. Благодаря ортогональности всех столбцов “матрицы ортогональных контрастов для комбинаторных планов” эти формулы имеют такой же простой вид, как и для планов 2 ^к.

В = ()^-1 у; тогда  b_i^g = 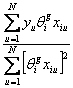;  S²{b_i^g} = ;  .

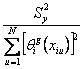Единственное отличие формулы для вычисления коэффициентов модели, в отличии от модели 2 ^к, состоит в том, что в знаменателе формулы вместо числа опытов N стоит сумма квадратов элементов столбца из матрицы контрастов.

После вычисления коэффициентов, дальнейший анализ проводится по схеме аналогичной для план 2 ^к. Все коэффициенты оцениваются независимо друг от друга (поскольку матрица контрастов ортогональна) с минимальными дисперсиями (но различными для каждого контраста) S ²{b_i^g}.