Методические указания к выполнению курсового проекта по курсу "Теория механизмов и машин", страница 68

Рис. 4.3.

В масштабе  изображаем звено 4 (рис. 4.3, а). В точке E на звено 4 со стороны звена 6 действует сила , которая равна по абсолютной величине и противоположна по направлению силе . Сила действия втулки 5 на звено 4  направлена перпендикулярно звену 4. Сила , действующая со стороны звена 2 на звено 4. Определив положение точки Д на отрезке ЕС, проводим из точки Д перпендикуляр к СД, а из точки Е - линию, параллельно EF.

В пересечении получим точку N. Соединяем точку N с точкой С. ДN изображает вектор силы , EN изображает вектор силы , а CN изображает вектор силы . Строим силовой многоугольник (рис. 4.3, б) в масштабе . Откладываем отрезок , изображающий вектор силы , с точки  откладываем линию параллельно вектору силы , а с точки  откладываем линию параллельно вектору силы . В пересечении получим точку . Из многоугольника находим две другие силы:

в) Группа Ассура 2-3 (рис. 4.4.)

Строим план ускорения рабочего положения в масшта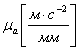бе . Изображаем звено АВ в масштабе . Это звено осуществляет плоско - параллельное движение. Прикладываем к нему силу инерции . Для этого найдем положение точки  на звене АВ, так как  лежит на звене 2 на одной линии между точками А и В, то на плане ускорений она также будет лежать на этой линии .

; откуда                          

Ускорение точки

Из точки  проводим линию  перпендикулярно АВ. Величину отрезка   находим следующим образом: по данным  определяем . А затем  . Соединяем точки В и N. Из точки N проводим линию перпендикулярно BN до пересечения с АВ в точке К. Из точки  проводим линию параллельно линии  из плана ускорений, а из точки К - параллельно линии  из плана ускорений. В пересечении этих линий получим точку Т. К