Методические указания к выполнению курсового проекта по курсу "Теория механизмов и машин", страница 18

Определим масштаб скорости для диаграммы  u , t , допустим, что u- среднее значение скорости точки С  за промежуток времени  2+3.

Тогда

u=

С учетом (3.13) имеем

откуда

Аналогично по диаграмме  u,t строится диаграмма  a_c=¦(t)  (рис. 1.3.2, в). Масштаб     ускорения диаграммы  a , t  в соответствии с формулой (1.3.14)

Если точка совершает криволинейное движение, то путем графического дифференцирования можно получить диаграмму тангенциальных (касательных ускорений).

Пример 2        Кривошипно- кулисно- ползунный механизм.

 

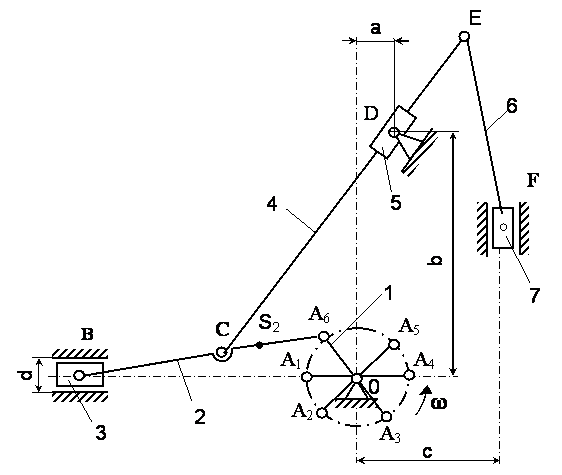Рис. 1.3.3

1.4.1 Построение плана положения звеньев и траектории движения                       отдельных точек механизма.

Для вычерчивания механизма в шести положениях используется масштаб плана механизма

         

Выбрав масштаб и определив чертежную величину каждого звена, выполняют построения положения механизма, для чего:

1)      Проводится окружность радиусом OA и делим окружность на шесть равных частей, начинаем с точки A¹ и против часовой стрелки через 60⁰ откладываем точки A₂,А₃,А₄,А₅ и А₆.

2)  Определить траекторию движения точки B |x-x|.

3)  Раствором циркуля A₁B₁ засекаем точку B на траектории x-x.                               И так от каждой точки А₂;А₃;А₄;А₅;А₆.

4)  Соединив найденные точки В₁;В₂;В₃;В₄;В₅ и В₆ и вычертив схематично ползун, получают положения механизма для точки B.

5)  На отрезке А₁В₁;А₂В₂; … А₆В₆ находим точку  С₁;С₂;С₃ … С₆ по отрезку А₁С₁.

6)  По координатам a и b находим точку D.

7)  Из точек С₁;С₂;С₃ … С₆ проводим отрезки СЕ через точку D. Получают точки E₁;E₂ … E₆. 

8)  Определить траекторию движения точки F  |x-x|.

9)  Раствором циркуля E₁F₁ засекаем точку  F₁  на траектории y-y по координате C.

10)  Соединив найденные точки  E₁ и F₁, и вычертив схематично ползун, получают положения механизма.

Ряд последовательных положений механизма, соответствующих различным значениям  j₀  (через 60⁰) на один оборот ведущего звена (цикла работы механизма) образует план положения механизма.

Линии, соединяющие на плане последовательные положения одноименных точек (например, С) называют траекторией движения этих точек.

1.4.2 Определение скоростей точек и звеньев механизма.

Точка А совершает вращательное движение вокруг неподвижного центра O

u_A=                (1.4.1)