Методические указания к выполнению курсового проекта по курсу "Теория механизмов и машин", страница 22

где    - ускорение точки С.

- нормальное ускорение точки Д относительно точки С.

- тангенциальное ускорение точки Д относительно точки С.

- ускорение камня, равное 0.

- ускорение Кориолиса.

Величину нормального ускорения  определяют по формуле

                                                                  (1.4.12)

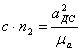
                                (1.4.13)

Из точки откладываем отрезок параллельно ДС в направлении от точки Д к точке С, изображающий в принятом масштабе нормальное ускорение . Затем через точку проводим линию перпендикулярно СД, которая изображает вектор тангенциального ускорения . Из полюса  откладываем отрезок     изображающий ускорение Кориолиса, для чего: вектор скорости точки  из плана скорости поворачиваем на 90⁰ в сторону вращения звена СЕ. Затем через точку  проводим линию перпендикулярно ; две линии действия пересекутся в точке . Соединив  и   на плане ускорений, получим отрезок - вектор относительного ускорения точки  при вращении вокруг точки . Соединив точку  с полюсом , получим абсолютное ускорение точки .

Точка  лежит на продолжении . Ее положение находим из подобия

;                             

Отложим отрезок , соединив полюс с точкой , получим ускорение точки    

Точка F совершает плоско – параллельное  движение. Для определения ускорения точки F разложим плоско – параллельное движение звена EF