Методические указания к выполнению курсового проекта по курсу "Теория механизмов и машин", страница 12

Вторая возможная кинематическая цепь из четырех звеньев и шести низших пар показана на рис. 2.1, д. Эта цепь присоединяется своими свободными элементами B и G.  В отличие от групп третьего класса, данная группа Ассура содержит два базисных звена, которые вместе с другими двумя звеньями образуют один подвижный четырехсторонний контур CEFД. Такие группы Ассура назвали группами четвертого класса второго порядка.

Механизмы, в состав которых входят группы не выше четвертого класса второго порядка, называются мех четвертого класса.

Третий возможный вид кинематической цепи из четырех звеньев и шести кинематических пар показан на рис. 2.1, е. Эта цепь распадается на две простейшие группы второго класса, поэтому относится к уже ранее рассмотренным и не представляет ничего принципиально нового. Следовательно, если в состав механизма входят группы Ассура различных классов, то класс определяется по той группе, которая относится к наивысшему классу.

При определении класса механизма необходимо указывать, какие звенья являются ведущими, ибо в зависимости от выбора ведущих звеньев может изменяться класс механизма. Деление механизма на группы Ассура следует всегда начинать с выходного звена (рис. 2.1, ж).

Если в состав механизма наряду с низшими кинематическими парами входят также и высшие, то, пользуясь методом замены высших пар низшими, всегда можно определить класс механизма.

1.3  Кинематический анализ механизмов.

          1.3.1. Задачи кинетического анализа механизмов.

Кинематический анализ предусматривает решение трех основных задач:

1)  Построение плана положения звеньев и траектории движения отдельных точек механизма.

2)  Определение скоростей точек  и звеньев механизма.

3)  Определение ускорений точек и звеньев механизма.

Указанные задачи можно решать аналитически, графоаналитически и графически. Выбор метода решения определяется степенью точности требуемого расчета. В настоящем методическом указании изложены графоаналитический и графический способ решения задач кинематики механизмов.

Начинать кинематический анализ следует с ведущего звена. Исходными условиями для решения задач кинематики являются: план положения механизма, геометрические параметры механизма, частота вращения ведущего звена.

1.3.2. Построение плана положения звеньев и траектории движения отдельных точек механизма.

Эту задачу можно сформулировать следующим образом: по известным геометрическим размерам механизма, задаваясь положением его ведущего звена, найти положение всех остальных звеньев. Основным методом решения данной задачи является метод геометрических мест (геометрических засечек). Сущность его рассмотрим на примере кривошипно-шатунного механизма (рис.1.3.1, а). Для  вычерчивания механизма используется кинематический масштаб длины

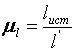                             [м/мм],

где          - истинная длина звена механизма;

                         - длина отрезка на чертеже, который изображает .,мм.

Масштаб длины подчиняется требованиям стандарта (ГОСТ 2.902-68); выражают его числами 1;2;2,5;4;5, ...   с нулями впереди либо сзади перед первой значащей цифрой, например: =0.02м/мм; =20 м/мм и т.д.

Выбрав масштаб и определив чертежную величину каждого звена, выполняют построение положения механизма, для чего:

1.  Радиусом АВ₁ описывают траекторию движения точки В (окружность).

2.  По заданной обобщенной координате    находят положение ведущего звена В.