Методические указания к выполнению курсового проекта по курсу "Теория механизмов и машин", страница 19

где    w= - угловая скорость звена

l_OA - радиус вращения;

n - частота вращения;

J_A ^ l_OA  и направлена в сторону мгновенного движения звена.

Масштаб скорости

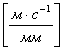;                                 (1.4.2)

где    u_A - абсолютное значение скорости, м/с

 - длина вектора абсолютной скорости на чертеже, мм.

Для построения плана скоростей по равенству берут произвольную точку p (полюс плана скоростей) и откладывают отрезок pa, который изображает вектор скорости.

Точка  B  совершает плоско – параллельное движение. Для определения скорости точки  B  разложим плоско – параллельное движение звена  AB на поступательное вместе с точкой  A  и вращательное вокруг точки  A.

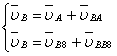   (1.4.3)  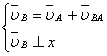               (1.4.4)      

где     - скорость точки А.

                          - скорость точки В при вращении звена АВ вокруг оси шарнира А.

                   ^ВА    

 - скорость точки    стойки 8, совпадающая с точкой В, она равна 0, так как звено 8 неподвижно.

- относительная скорость точки В в ее движении относительно точки      (ее модуль неизвестен, а направлена она вдоль линии  ВХ (по оси x)).

Построение следующее. Из точки  проводим линию ^АВ, а из полюса Р линию параллельно оси Х. В пересечении получим точку .

Скорость точки В равна

Точка С.  Скорость точки С звена АВ находим по правилу подобия 

;             

На отрезке  откладываем полученное значение . Соединив точку  с полюсом  получаем вектор , который в масштабе является скоростью     точки С.

Точка Д совершает плоско – параллельное движение: поступательное вместе с точкой С и вращательное вокруг точки С.

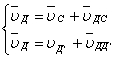                      (1.4.5)

где   - скорость точки Д 

       - скорость точки Д относительно точки С, направлена перпендикулярно звену СД.

       - скорость точки Д' относительно Д.

       - скорость звена 4 относительно точки Д, направлена вдоль               звена СД.

Построение следующее. Из точки С проводим линию перпендикулярно СД, а из полюса  проводим линию параллельную СД в пересечении получим      точку .