Методические указания к выполнению курсового проекта по курсу "Теория механизмов и машин", страница 40

2.46.  Каким методом строится диаграмма перемещения?

2.47.  Каким способом строятся диаграммы скорости и перемещения?

2.48.  В чем заключается динамический синтез плоского кулачкового механизма?

2.49.  Где применяют кулачковые механизмы?

ПРИЛОЖЕНИЕ 2

Пример расчета 2 листа:

2а) Динамический синтез плоского     кулачкового механизма с коромыслом.

   2б) Динамический синтез плоского   кулачкового механизма с  толкателем.

2а     Динамический синтез плоского кулачкового механизма с коромыслом.

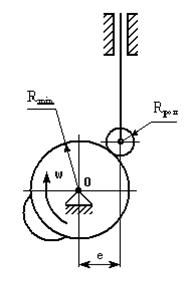Дано:      ОА=25мм

                                                 

                                                   

                                                  
                                                                                      

Дано:

К₁=1/4

К₂=1/8

К₃=1/8

К₄=1/2

2. Динамический синтез плоского кулачкового механизма с коромыслом.

Задача синтеза кулачкового механизма состоит в построении профиля кулачковой шайбы, удовлетворяющего поставленным технологическим процессом требованиям.

2.1. Построение диаграмм движения.

Синтез кулачкового механизма начинаем с построения диаграммы движения ведомого звена – коромысла , исходя из заданной диаграммы ускорения. За величину амплитуды диаграммы ускорений на участке  принимаем отрезок  произвольной длины (20мм).

Т.к. угол удаления  не равен углу возврата , . Для определения амплитуды  на участке  воспользуемся уравнением:

            

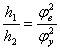
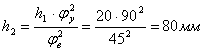
Интегрируя графически диаграмму ускорений (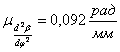) получаем диаграмму скорости (). Для этого проводим следующие построения:

1) Строим на отрезке …соответствующие срединам интервалов                  16-17, 17-18, … Откладываем отрезки … на оси ординат.

2) Соединяем произвольно взятую точку  на расстоянии  от начала координат на продолжении оси абсцисс, с точками ,… ().

3) Из точки 16' диаграммы скоростей проводим отрезок 16'17' параллельно лучу  в интервале 16-17, из точки 17' – параллельно лучу  в интервале 17-18 отрезок 17'18' и т.д. Полученная ломаная линия представляет собой первый интеграл заданной зависимости. Аналогично интегрируя диаграмму скорости, получим диаграмму перемещений (). .