Методические указания к выполнению курсового проекта по курсу "Теория механизмов и машин", страница 17

Кинематические диаграмма – графическое изображение функциональной зависимости перемещения, скорости, ускорения точки или угла поворота, угловой скорости и углового ускорения тела от заданного параметра. Таким заданным параметром могут быть время и угол поворота ведущего звена в течении одного цикла движения механизма. Кинематические диаграммы скоростей и ускорений строят обычно либо по данным планов скоростей и ускорений, либо графическим дифференцированием диаграммы перемещений  S=(t).

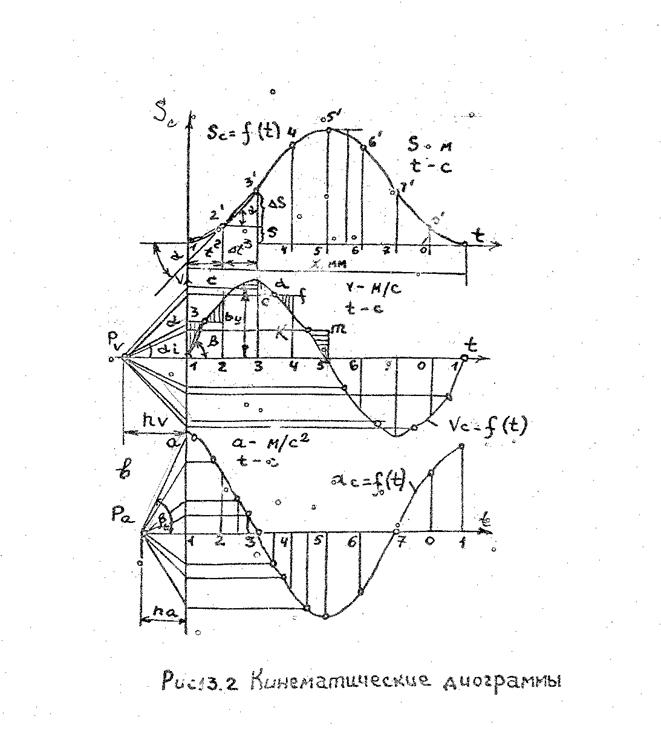
Рассмотрим метод графического дифференцирования применительно к кривошипно-ползунному механизму  (рис. 1.3.1, а).

Согласно плану положения механизма построим диаграмму S_C=(t)              перемещения точки C за один цикл движения ведущего звена. Отчет перемещения точки  C  лучше всего вести от одного из крайних положений ползуна, например от правого. По оси абсцисс системы координат S,t (рис. 1.3.2, а) отложим отрезок  (мм), изображающий в масштабе  время одного оборота кривошипа   и, следовательно, масштаб времени

 ,  [c/мм]

Масштаб времени должен подчинятся требованиям ГОСТ 2.302-68. Отрезок    делим на то же число равных частей, что и траекторию точки B. Через

полученные точки 1, 2, 3 … проводят прямые, параллельные оси координат. На этих прямых откладывают величину перемещения точки С за время движения ведущего звена от одного к другому положению, т.е. отрезки С1С2;С2С3;С3С4 … , длину которых измеряем непосредственно на плане положения механизма. Таким образом, получим точки , , , … , соединив которые получим диаграмму S_C=(t) в масштабе . В целом масштаб перемещений определяется по формуле

Из этой формулы видно, что  = если 2. Путь, пройденный точкой C за цикл движения S_C=2 (рис. 1.3.2, а).

Координаты любой точки полученной кривой, например 2, будут равны:

;         

Определить среднюю скорость движения точки C за промежуток времени :

u=                      (1.3.13)

где  a - угол, образуемый хордой 2¢3¢ с осью времени (рис. 1.3.2, а).

Аналогично, имея график  u=¦(t), можно определить среднее за рассматриваемый интервал времени тангенциальное ускорение точки

где    b - угол наклона на графике  u , t  хорды (например, 23) к оси времени        (рис. 1.3.2, б).

Итак, задана диаграмма  S_c=¦(t)  (рис. 1.3.2, а), требуется построить диаграмму  u_c=¦(t). Масштаб   времени принимаем для них общим.

В пределах каждого из интервалов 1-2, 2-3, … кривую  S_c=¦(t)  заменим ломаной линией (совокупность хорд каждого элементарного участка). На продолжении оси абсцисс диаграммы u_c=¦(t)  влево от начала координат выбираем полюс P_u  и проводим через него лучи, параллельные хордам 1-2, 2-3, 3-4, … диаграммы S_c=¦(t). Лучи отсекают на оси отрезки, пропорциональные средним скоростям точки С за рассматриваемый промежуток времени. Принимая полученные отрезки за ординаты диаграммы  (u,t), построим ее в виде ступенчатой линии abcdefkm  (рис. 1.3.2,б). Если промежуток времени 1+2, 2+3, 3+4, … достаточно малы, то можно считать, что точки кривой       находятся на серединах соответствующих ступеней линии abcdefkm, Рассматривая вторую половину кривой u_c=¦(t)  на участке  5¢6¢7¢  аналогично строят вторую часть кривой S_c=¦(t)