Методические указания к выполнению курсового проекта по курсу "Теория механизмов и машин", страница 51

Кинематическая схема на рис. 3.1, в имеет центральные колеса и , блок сателлитов из колес и  и водило . При малой разности в числах  и  на блоке сателлита передача имеет очень большие передаточные отношения  в пределах до 1000. Передачи с двумя внешними зацеплениями имеют более низкий КПД и применяются редко.

Кинематическая схема (рис. 3.1, г) представляет собой соединение более простых кинематических схем, рассмотренных выше. Так, в кинематической схеме на рис. 3.1,б последовательно соединены две однорядные планетарные передачи, аналогичные кинематической схеме по рис. 3.1,а. Передаточное отношение  такой передачи достаточно большое (до 80) при высоком значении КПД (h=0,90…0,96).

Число сателлитов назначают в переделах . При этом условии необходимо выполнять условия соседства двух смежных сателлитов по межосевому расстоянию

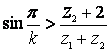                (3.1)

Условия сборки сателлитов

          (3.2)

где    - число зубьев центрального колеса

          – передаточное отношение от входного звена  к выходному                 звену – водилу.

          – число сателлитов; - целое число; 0; 1; 2; 3; … - целое число. 

Условие соосности

схема а:     

схема б:    

         схема в:                                    (3.3)

схема г:     

3.2.  Методические указания.

3.2.1. Для вывода формулы передаточного отношения нужно изучить заданную кинематическую схему механизма и разбить ее на структурно неделимые части (простой зубчатый механизм, планетарный механизм и т.д.), которые соединяются между собой последовательно. Выводятся передаточные отношения каждой части и записывается общее передаточное отношение как произведение передаточных отношений структурных частей через число зубьев. Для планетарной части передаточное отношение выводится по формуле Виллиса.

3.2.2. Производится разбивка общего передаточного отношения по структурным частям, исходя из следующего:

-  передаточное отношение внешнего зацепления должно быть до 5;

-  передаточное отношение внутреннего зацепления должно быть до 5…8; 

-  передаточное отношение планетарного механизма зависит от его кинематической схемы и числа сателлитов и может быть принято из диапазона, представленного в приложениях 1,2,3 и 4.

-  если задано последовательное соединение нескольких одинаковых планетарных механизмов, то можно принять равные передаточные отношения каждого из них.

3.2.3. Подбор чисел зубьев планетарного редуктора производится с одновременным выполнением трех обязательных условий (уравнения 3.1, 3.2 и 3.3)