Методические указания к выполнению курсового проекта по курсу "Теория механизмов и машин", страница 15

по направлению  R                            (1.3.6)

и направлено к центру вращения.

Если звено совершает плоскопараллельное движение, то ускорение любой его точки (например, точки В) состоит из переносного и относительного ускорений, что можно записать:

               _B       (1.3.7)   

где    ,  - соответственно нормальная и тангенциальная составляющая относительного ускорения.  R, ^R, R - радиус вращения рассматриваемой точки. Аналогично уравнению (1.3.6) =R, т.е. относительное нормальное ускорение любой точки звена, совершающего плоскопараллельное движение, всегда можно определить используя выражение (1.3.6)

Рассмотрим методику решения задач по определению ускорений и звеньев механизма на примере шарнирного четырехзвенника (рис. 1.3.1, б). Исходными данными для решения настоящей задачи являются:

1.  План положения механизма (рис.1.3.1, б);

2.  Геометрические параметры механизма;

3.  Частота вращения ведущего звена;

4.  План скоростей рассматриваемого механизма.

Точка В совершает вращательное движение вокруг точки механизма, следовательно, с учетом (1.3.6)

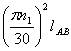_B==;     u_B  

Рассматривая точку С по отношению точек  В  и  Д  с учетом характера движения звеньев   2 и 3, в соответствии с уравнением (1.3.7) запишем:

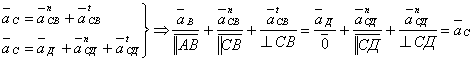   (1.3.8)

Полученное равенство решают графически путем построения плана ускорений, предварительно определив  и , значение которых равно:

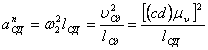
Значения ,, u_CB, u_СД были определены в пункте 3.3.

Для построения плана ускорения механизма выбирают кинематический масштаб ускорений:

,       

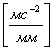
где     - абсолютное ускорение рассматриваемой точки, м/с²;

- длина вектора абсолютного ускорения на чертеже, мм.

Масштаб ускорения должен соответствовать требованиям ГОСТ 2.302-68.

План ускорений строят при точке     (полюс плана ускорений) согласно равенству (1.3.8). Пересечение векторов   и    определяет положение точки С (рис.1.3.1, г). Соединив точку С с полюсом плана ускорений получаем вектор абсолютного ускорения точки С. Абсолютное ускорение точки С будет равно:

,                 [м/с²]

Построив план ускорений, согласно (1.3.8) определяют:

;

;

.

Для определения ускорения точки Е рассматривают ее движение относительно точек В и С, скорости которых уже известны.