Методические указания к выполнению курсового проекта по курсу "Теория механизмов и машин", страница 16

На основании (1.3) имеем:

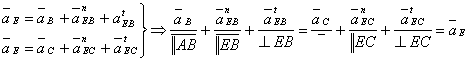  (1.3.10)

Определив значения

И строя план ускорений согласно равенству (1.3.10), получают вектор ускорения точки Е (рис.1.3.1, г). Абсолютные значения ускорений будет равны:

        ;     ;      ;     .

Конец вектора ускорений точек  Е  можно построить геометрически, для чего на векторе относительного ускорения  при точках c и b необходимо  построить соответственно углы b  и a. Пересечения лучей этих определить точку  на плане ускорений.

Свойства плана ускорений:

1.  Векторы, имеющие свои началом полюс плана ускорений, -  векторы абсолютных ускорений рассматриваемых точек;

2.  Отрезки, соединяющие концы векторов абсолютных ускорений, - векторы относительных ускорений рассматриваемых точек;

3.  План ускорений звена подобен его геометрическому очертанию, сходственно с ним расположен, но повернут на угол 180⁰-l   а сторону мгновенного вращения звена.

tgl=l=arctg

Значение тангенциальной составляющей ускорения

,

где    - рассматриваемые точки звеньев механизма; 

 - угловое ускорение   -го звена, р/с;

 - длина звена между точками .

Используя уравнение (1.3.12) и план ускорений (рис. 13.1, г) или (1.3.9),(1.3.11), определяют угловое ускорение любого звена механизма, которое соответственно будет равно: 

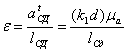
Направление углового ускорения  определяются вектором  относительного тангенциального ускорения рассматриваемых точек, если последние перенести параллельно самому себе не меняя его направления с плана ускорения в рассматриваемую точку механизма.

Например, определяя направление , вектор тангенциального ускорения (направлена от  к на плане ускорений) переносят параллельно самому себе В рассматриваемую точку  С  механизма. Точку С по отношение точки В вектор     стремится повернуть против хода часовой стрелки, следовательно  направлено против часовой стрелки. Аналогично определяют направление по вектору .  направлено против часовой стрелки. Если направление угловой скорости и углового ускорения совпадает, значит, звено движется ускоренно, если эти векторы противонаправлены, то движение звена замедленное.

1.3.5 Кинематический анализ механизмов методом диаграмм.