![]()
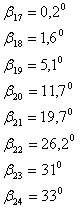
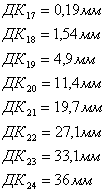
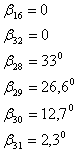
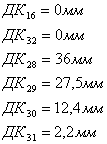
Лучи
![]() представляют собой мгновенные
положения коромысла при его перемещении в соответствии с заданным законом
движения, а точки пересечения этих лучей с дугой
представляют собой мгновенные
положения коромысла при его перемещении в соответствии с заданным законом
движения, а точки пересечения этих лучей с дугой ![]() определяют положение центра
ролика. На лучах
определяют положение центра
ролика. На лучах ![]() от точки пересечения их с
дугой
от точки пересечения их с
дугой ![]() откладываем
отрезки
откладываем
отрезки ![]() ,
изображающие соответствующие значения величины
,
изображающие соответствующие значения величины ![]() в
масштабе
в
масштабе ![]() .
Величины этих отрезков определяем по формуле
.
Величины этих отрезков определяем по формуле
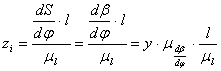
![]() - величина первой производной
линейного перемещения центра ролика коромысла по углу поворота кулачка.
- величина первой производной
линейного перемещения центра ролика коромысла по углу поворота кулачка.
![]() - величина первой производной
углового перемещения коромысла по углу поворота кулачка.
- величина первой производной
углового перемещения коромысла по углу поворота кулачка.
![]() - масштаб диаграммы функции
- масштаб диаграммы функции
![]() .
.
![]() - длина коромысла в
- длина коромысла в ![]() .
.
![]() - масштаб чертежа.
- масштаб чертежа.
Длины
отрезков ![]() определяем
графически, методом пропорционального деления. Для этого определим величину
наибольшего отрезка при удалении коромысла:
определяем
графически, методом пропорционального деления. Для этого определим величину
наибольшего отрезка при удалении коромысла:
![]()
![]()
Полученный
отрезок откладываем на стороне произвольного угла ![]() . На другой стороне угла
откладываем ординату точки
. На другой стороне угла
откладываем ординату точки ![]() диаграммы
скорости
диаграммы
скорости ![]() ,
принадлежащей участку подъема диаграммы соединяем полученные точки
,
принадлежащей участку подъема диаграммы соединяем полученные точки ![]() и
и ![]() .
На второй стороне угла откладываем ординаты оставшихся точек участка подъема
диаграммы скорости
.
На второй стороне угла откладываем ординаты оставшихся точек участка подъема
диаграммы скорости ![]() . Из этих точек проводим
отрезки параллельно
. Из этих точек проводим
отрезки параллельно ![]() , в пересечении с первой
стороной угла получим точки
, в пересечении с первой
стороной угла получим точки ![]() . Найдем искомые
длины отрезков
. Найдем искомые
длины отрезков ![]() …
…
Аналогично
определяем величины отрезков ![]() при
возвращении коромысла
при
возвращении коромысла
![]()
![]()
![]()
Направление
вращения кулачка принимаем противоположно направлению вращения коромысла при
его удалении, ![]() откладываем вправо от дуги
откладываем вправо от дуги
![]() при
удалении коромысла, а
при
удалении коромысла, а ![]() влево при его возвращении.
Соединив последовательно
влево при его возвращении.
Соединив последовательно ![]() … плавной кривой
получим геометрическое место концов отрезков
… плавной кривой
получим геометрическое место концов отрезков ![]() .
Через крайние точки
.
Через крайние точки ![]() и
и ![]() проводим
прямые под углом
проводим
прямые под углом ![]() . В пересечении этих прямых
получим треугольник – область центра вращения кулачка. Пусть центр вращения
кулачка
. В пересечении этих прямых
получим треугольник – область центра вращения кулачка. Пусть центр вращения
кулачка ![]() , принадлежащая этой области
, принадлежащая этой области
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.