Методические указания к выполнению курсового проекта по курсу "Теория механизмов и машин", страница 21

1.4.3  Определение ускорений точек и звеньев механизма.

Точка A совершает вращательное движение вокруг неподвижного центра O, поэтому ускорение определяется по формуле

;                          (1.4.7)

где  параллельно AO и направлено от точки A к точке O.

Масштаб ускорения

;            

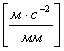
Для построения плана скоростей берут произвольную точку  (полюс плана ускорений) и откладывают отрезок , который изображает вектор ускорения .

Точка B совершает плоско – параллельное движение. Для определения ускорения точки B разложим плоско – параллельное движение звена AB.

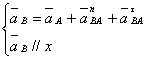                    (1.4.9)

где     - абсолютное ускорение точки B.

 - нормальное ускорение точки B при вращении вокруг точки A. Направлена параллельно AB в направлении от точки B к точке A.

 - тангенциальное ускорение точки B при вращении вокруг точки A    направлено перпендикулярно AB.

Величину нормального ускорения  определяют по формуле

                              (1.4.10)

Отложим отрезок  , изображающий в принятом масштабе нормальное ускорение в направлении от точки B к точки A. Затем через точку  проведем линию перпендикулярно AB, которая изображает вектор тангенциального ускорения  .После этого, рассматриваем точку B как принадлежащую поршню, совершающему абсолютное прямолинейное поступательное движение по линии OB (оси x), проведем из полюса прямую, параллельно OB; две линии действия пересекаются в точке . Соединив точки    и  на плане ускорений, получим отрезок -вектор относительного ускорения точки  при вращении вокруг точки .

Ускорение точки C определяется при помощи теоремы подобия, из которой следует, что

;                 

Отложим отрезок , соединим полюс  с точкой , получим ускорение точки .

Ускорение точки Д.

Для определения ускорения точки Д, используем векторные уравнения

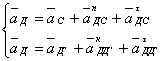                    (1.4.11)