Методические указания к выполнению курсового проекта по курсу "Теория механизмов и машин", страница 29

1.2  Построение плана ускорений.

Так как  , то ускорение точки А определяем по формуле

Из полюса    плана ускорений отложим отрезок    в направлении от А₁  к О₁. Этот отрезок изображает ускорение точки А    в масштабе

Для определения ускорения точки В₁   используем векторное уравнение, основанное на идее разложения плоско - параллельного движения звена А₁В₁.

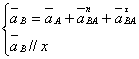
где     - вектор нормального ускорения точки  В₁  в ее вращательном   относительном движении вокруг точки А₁, направленный от точки В₁ к точкеА₁.

 - вектор тангенциального ускорения точки В в том же  движении , перпендикулярном АВ.

 - вектор абсолютного ускорения точки В.

Величину нормального ускорения    определяют по формуле:

Длина отрезка  , направлен от точки В₁ к точке А₁ параллельно звену В₁А₁.

Через точку n₁  проводим перпендикуляр к А₁В₁, а через полюс  - линию, параллельно  и в пересечении получаем точку b1.

Точку С находим из пропорции

;         

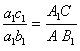Для определения ускорения точки Д₁ используем векторные уравнения.

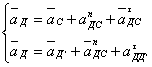
где     - ускорение точки С

          - нормальное ускорение точки Д относительно точки С.

                   - тангенциальное ускорение точки Д относительно точки С.

                    - ускорение камня, равное 0

          - вектор Кариолисова ускорения: откладывается поворотом вектора скорости точки Д на 90⁰ в сторону вращения звена Е₁С₁. На чертеже этот отрезок обозначается .

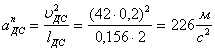
    откладываем из точки С₁ параллельно Д₁С₁.

Из точки  откладываем прямую, перпендикулярную звену С₁Д₁, из точки  - прямую, перпендикулярную . На пересечении этих прямых получаем точку .