Машиностроение \ Теория механизмов и машин

Методические указания к выполнению курсового проекта по курсу "Теория механизмов и машин", страница 13

3.  Определить траекторию движения точки С (x-x).

4.  Раствором циркуля В0С0 засекают точку  С0 на траектории x-x.

5.  Соединив найденные точки В0 и С0 и вычертив схематично ползун, получают положение механизма для заданного значения .

Ряд последовательных положений механизма, соответствующих различным значениям     на один оборот ведущего звена (цикл работы механизма) образует план положения механизма (рис. 1.3.1, а).

Линии, соединяющие на плане последовательные положения одноименных точек (например, точки Е рис. 1.3.1, а) называют траекторией движения этих точек.

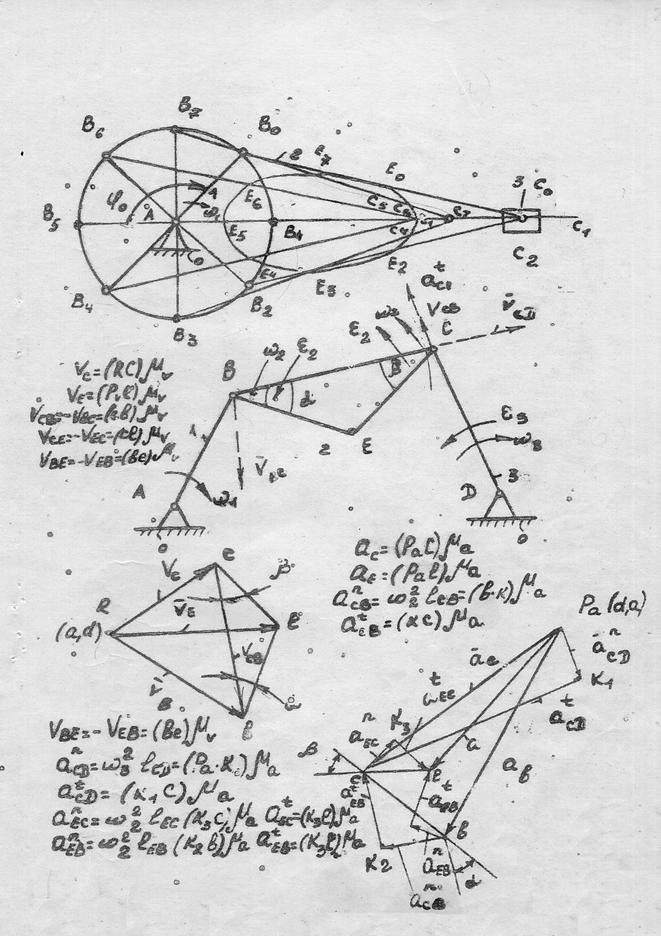
Рис. 1.3.1

1.3.3. Определение скоростей точек и звеньев механизма.

Скорости точек и звеньев механизма определяют по известным правилам теоретической механики в зависимости  от характера движения звеньев.

При поступательном движении звена  скорости всех точек его будут равны и направлены в одну сторону, т.е.:

;      

При вращении звена вокруг неподвижного центра скорости точек его связаны зависимостью

u=

где     - угловая скорость  звена, р/с;

n  - частота вращения звена;

R - радиус вращения, м, u^R и направлен в сторону мгновенного движения     звена. 

Если звено совершает плоскопараллельное движение, то линейная скорость любой его точки (например, точки В) выражается уравнением

uВ=uпер+uотн=uпер+R

Где uпер, uотн - соответственно векторы переносной и относительной скорости точек рассматриваемого звена. uотн перпендикулярен R и направлен в сторону мгновенного вращения звена.

Рассмотрим методику решения задач по определению скоростей  точек и звеньев механизма на примере шарнирного четырехзвенника. Исходными данными для решения настоящей задачи являются:

1.  План положения механизма (рис. 1.3.1, б);

2.  Геометрические параметры механизма;

3.  Частота вращения ведущего звена (n1).

Точка В механизма принадлежит звену 1 и вращается вокруг неподвижной точки А, следовательно, с учетом уравнения (1.3.1):

uB=,    uB^

Рассматривая точку С по отношению точек В и Д, с учетом характера движения звеньев 2 и 3, в соответствие уравнением (3.2), запишем:

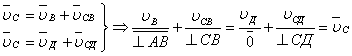
Из анализа равенства (1.3.3) видно, что оно решается только графически путем построения плана скоростей.

Для построения последнего выбирают кинематический масштаб скорости

     

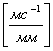
где    uист - абсолютное значение скорости, м/с;

                    - длина вектора абсолютной скорости на чертеже, мм.

            Масштаб скорости подчиняется требованиям ГОСТ 2.302-68.

Для построения плана скоростей по равенству (1.3.3) берут произвольную точку Pu         (полюс плана скоростей) и строят векторы скоростей, входящих в равенство с учетом их направления. Точка пересечения  известных по направления векторов равенства (1.3.3) определяет конец вектора скорости искомой точки С (рис. 3.1, в). Вектор  Pu C-вектор скорости точки С в масштабе , следовательно:

Скачать файл