Методические указания к выполнению курсового проекта по курсу "Теория механизмов и машин", страница 34

Указания к выполнению задания 2 листа.

Выбор варианта задания см. раздел 1. Варианты заданий на курсовой проект по ТММ. Задания ко 2-му листу см. выше.

Объем выполнения второго листа.

1). Определяются фазовые углы и амплитуда на участках.

2). Построение диаграммы ускорения.

3). Построение диаграммы скорости.

4). Построение диаграммы перемещений методом графического интегрирования.

5). Определение минимального радиуса кулачка.

6). Профилирование кулачка.

Расчет и оформление 2 листа.

Расчет задания осуществляется согласно раздела 2 настоящего методического пособия. Расчетные формулы применительно к расчетному механизму приводятся на листах с арифметическими расчетами.

Графическая часть выполняется на ватмане формата А1.

2.  Динамический синтез кулачкового механизма с коромыслом

(см. приложение 2 лист 2)

2.2 Построение диаграмм движения.

Синтез кулачкового механизма начинаем с построения диаграмм движения ОА – коромысла исходя из заданной диаграммы   .  

За величину амплитуды диаграммы ускорений на участке  принимаем отрезок  произвольной длины (20 или 30 мм). Если углы  и  равны, то . Если углы   то для определения амплитуды воспользуемся уравнением 

,

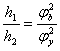откуда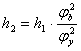    

Фазовые углы определяются

-угол удаления (поднятия)

-угол верхнего выстоя

-угол возврата (опускания)

-угол нижнего выстоя

где    

 по заданию задаются.

Интегрируя графически диаграмму ускорений , получаем график .

Для этого проводим следующие построения:

2.2.1 Строим отрезки ,   … соответствующие серединам интервалов 16-17, 17-18, … откладываем отрезки ,  … на оси ординат.

2.2.2 Соединяем произвольно взятую точку  на расстоянии от начала координат на продолжении оси абсцисс, с точками , …( или   или ).   

2.2.3  Из точки 16' диаграммы скоростей проводим отрезок 16'17' параллельно лучу  в интервале 16-17 из точки 17'- параллельно лучу  в интервале 17-18 отрезок 17'18' и т.д. Полученная ломаная линия представляет собой первый интеграл заданной зависимости. Аналогично интегрирую диаграмму скорости, получим диаграмму перемещений . Полюсное расстояние принимаем  (или ).