Воспользовавшись принципом перестановочной двойственности, из соотношений (3.9), (3.10) получим следующие выражения для поперечно электрического поля ТЕ(Н) относительно z:
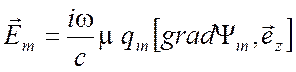 ,
(3.15)
,
(3.15)
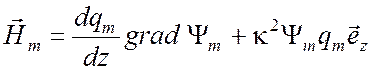 .
(3.16)
.
(3.16)
Электрическое поле имеет одну касательную составляющую
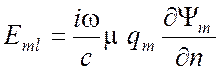 .
.
Таким образом, граничное условие (3.2) сводится к условию
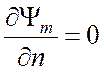 на
С, (3.17)
на
С, (3.17)
и для мембранной функции ![]() имеем граничную задачу Неймана: ищется
решение уравнения (3.7) совместно с граничными условиями (3.17).
имеем граничную задачу Неймана: ищется
решение уравнения (3.7) совместно с граничными условиями (3.17).
Данная граничная задача для
функции ![]() имеет нетривиальное решение лишь при
некоторых собственных значениях
имеет нетривиальное решение лишь при
некоторых собственных значениях ![]() , … ,
, … , ![]() , … , образующих ее спектр (вообще говоря,
отличный от спектра рассмотренной выше задачи Дирихле). Эти собственные
значения также образуют возрастающую (точнее, неубывающую) последовательность.
Каждому собственному значению
, … , образующих ее спектр (вообще говоря,
отличный от спектра рассмотренной выше задачи Дирихле). Эти собственные
значения также образуют возрастающую (точнее, неубывающую) последовательность.
Каждому собственному значению ![]() соответствует
некоторая собственная функция
соответствует
некоторая собственная функция ![]() , дающая распределение
поля данной магнитной волны, и продольное волновое число
, дающая распределение
поля данной магнитной волны, и продольное волновое число ![]() . Для магнитных волн соотношения
(3.12) - (3.14) также справедливы, в частности распространение или затухание
данной волны имеет место в зависимости от соотношения между рабочей длиной
волны
. Для магнитных волн соотношения
(3.12) - (3.14) также справедливы, в частности распространение или затухание
данной волны имеет место в зависимости от соотношения между рабочей длиной
волны ![]() и критической волной
и критической волной ![]() . Последняя зависит лишь от
геометрии поперечного сечения и от номера магнитной волны. Заметим, что в число
собственных значений не включено значение
. Последняя зависит лишь от
геометрии поперечного сечения и от номера магнитной волны. Заметим, что в число
собственных значений не включено значение ![]() = 0, которому
соответствует собственная функция
= 0, которому
соответствует собственная функция ![]() = const,
удовлетворяющая уравнению (3.7) и условию (3.17). Действительно, такая
собственная функция приводит по формулам (3.15) , (3.16) к электромагнитному
полю, тождественно равному нулю, и потому не представляет интереса.
= const,
удовлетворяющая уравнению (3.7) и условию (3.17). Действительно, такая
собственная функция приводит по формулам (3.15) , (3.16) к электромагнитному
полю, тождественно равному нулю, и потому не представляет интереса.
Изложенная выше теория электрических и магнитных волн в волноводах показывает, что потенциалы облегчают решение электродинамических задач. В самом деле, с помощью электрического и магнитного векторов Герца задача об электромагнитных волнах в волноводе произвольного поперечного сечения сведена к двум граничным задачам для двумерного волнового уравнения. Эти задачи давно исследованы в связи с другими физическими проблемами. В следующих параграфах изложенная выше общая теория электрических волн в волноводе с произвольным поперечным сечением будет применена к волноводам с прямоугольным и круговым сечениями.
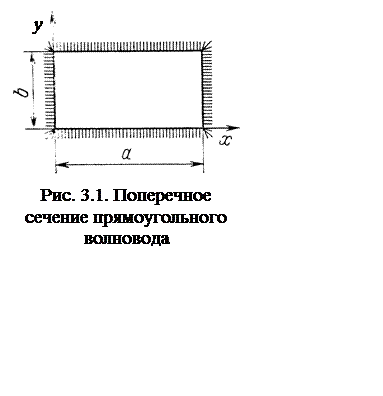
Выберем начало координат в одной
из вершин прямоугольного поперечного сечения и направим ось х вдоль
большей стороны а, а ось у - вдоль меньшей стороны b прямоугольника (рис. 3.1).
Будем искать решение двумерного волнового уравнения (3.7) методом разделения
переменных: а именно напишем для функции ![]() выражение
выражение
![]() (3.18)
(3.18)
 и подставим его в уравнение (3.7). После деления обеих частей
уравнения на произведение XY получим
и подставим его в уравнение (3.7). После деления обеих частей
уравнения на произведение XY получим
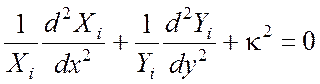 .
(3.19)
.
(3.19)
Из последнего соотношения следует, что каждое слагаемое
должно быть постоянной величиной; обозначим эти постоянные через ![]() и
и ![]() соответственно.
В результате приходим к двум уравнениям
соответственно.
В результате приходим к двум уравнениям
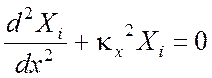 ,
,
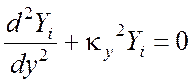 (3.20)
(3.20)
где в силу соотношения (3.19) должно выполняться равенство
![]() ,
(3.21)
,
(3.21)
которое можно рассматривать как продолжение разложения ![]() , а именно разложение поперечного вектора
, а именно разложение поперечного вектора ![]() на
составляющие
на
составляющие ![]() и
и ![]() ,каждая из которых определяет зависимость
потенциалов и полей от поперечной координаты х или у.
,каждая из которых определяет зависимость
потенциалов и полей от поперечной координаты х или у.
Общие решения уравнений (3.20) имеют вид
![]() ,
, ![]() ,
(3.22)
,
(3.22)
где A1i, A2i, B1i и
В2i суть произвольные постоянные. Функция ![]() должна удовлетворять граничным
условиям (3.11), (3.17). Рассмотрим сначала случай ТМ(Е) поля. Имеем
должна удовлетворять граничным
условиям (3.11), (3.17). Рассмотрим сначала случай ТМ(Е) поля. Имеем
![]() при
х = 0 и х = а, у = 0 и у = b,(3.23)
при
х = 0 и х = а, у = 0 и у = b,(3.23)
и функции Xе и Yе должны удовлетворять следующим соотношениям:
Хе = 0 при х = 0, откуда А1е = 0;
Хе = 0при х = а, откуда![]() ;
;
Yе = 0при y = 0, откуда B1e = 0;
Yе = 0при
y = b,
откуда ![]() .
.
Для
того чтобы получить нетривиальное решение граничной задачи, необходимо
выбрать числа ![]() и
и ![]() так,
чтобы они удовлетворяли уравнениям
так,
чтобы они удовлетворяли уравнениям
![]() ,
, ![]()
т. е. взять
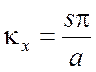 и
и
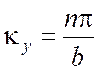 ,(3.24)
,(3.24)
где s и п суть целые числа 1, 2, 3, ... Таким образом, получаем собственные функции данной граничной задачи в виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.