Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 8

и, учитывая гармоническую зависимость от времени, получаем решения вида

.

Таким образом, волновая функция представляет собой плоскую волну, распространяющуюся в положительном или отрицательном направлении z. Волновая функция одинакова для всех волноводов, а мембранная функция зависит от конфигурации волновода (поперечного сечения).

Запишем выражения для поперечно магнитного поля ТМ(Е) относительно координаты разделения z.

Воспользуемся соотношениями

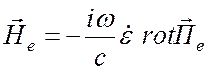 , ,                        (1.56)

Подставим в них выражение (3.5) и распишем операции градиента, дивергенции и ротора, воспользовавшись формулами (П1.1) – (П1.4) Приложения 1. В результате получим следующие выражения:

,                                  (3.9)

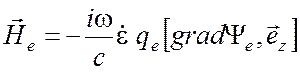                                    (3.10)

Граничное условие (3.2) на идеально прово­дящей стенке волновода будет  выполняться,  если  функция  удовлетворяет граничному условию

 на С.                                                (3.11)

Действительно, если ввести вектор нормали  и касательный к поверхности волновода вектор  так, что орты  образуют правую систему, то касательными к поверхности волновода направлениями будут  и . Расписав компоненты электрического поля  получим выражения:

, ,

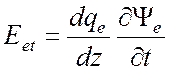которые выполняются одновременно при выполнении условия (3.11).

Таким образом, для мембранной функции , которая удовлетворяет двумерному уравнению (3.7) и граничному условию (3.11), приходим к так называемой задаче Дирихле.

Данная граничная задача для функции  имеет нетривиальное решение не при любых значениях поперечного волнового числа , а лишь при некоторых , , … , , … , образующих спектр собствен­ных значений данной граничной задачи. Величины образуют возрастающую (или, по крайней мере, неубывающую) последова­тельность положительных вещественных чисел. Каждому собст­венному значению поперечного волнового числа соответствуют два значения продольного волнового числа

                                                   (3.12)

и некоторая собственная функция .

Так как  значение h² может быть как положительным, так и отрицательным, то в первом случае получаем волну с вещественным волновым числом h (3.12). Эта волна распространяется вдоль волновода без затухания, так как потерями в   стенках волновода пренебрегаем и считаем их идеально проводящими. Во втором случае волновое число h получается чисто мнимым:

                                                (3.13)

и волна затухает, не распространяясь. Заметим, что это затухание не связано с какими-либо потерями.

Исследуем подробнее, при каких условиях данная волна в вол­новоде распространяется, а при каких затухает. Для этого положим 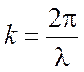, где в соответствии с формулой (2.14)  есть длина вол­ны в свободном пространстве. Будем далее считать, что волна рас­пространяется, возьмем в формуле (3.12) знак плюс и введем длину волны в волноводе по формуле 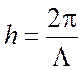. Длина волны  определяет периодичность поля распространяющейся волны по оси z. Если так же определить критическую  длину волны  по формуле 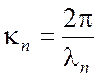 (считаем > 0), то соотношение  (3.12)  при­мет вид

                                                                    (3.14)

Данная волна является распространяющейся только при , т.е. когда длина волны меньше критической. Если же, наоборот, длина волны больше критической (), то волна является за­тухающей и ее волновое число определяется формулой (3.13). Такие волны также называются местными. О длине волны в волноводе в этом случае вообще говорить нельзя, так как поле теряет волновой характер.

Критической длиной волны  (или критическим волновым числом ) называется потому, что при не­прерывном изменении  при  происходит качественное изме­нение - данная волна из распространяющейся становится местной или наоборот.

При  (или ) все волны местные. Как только  в волноводе возникает одна распространяющаяся волна. При  в волноводе имеется две распространяющиеся волны и т.д. Каждое собственное значение определяется лишь геометри­ей поперечного сечения волновода - его размерами и формой. То же относится и к критической длине волны . С другой стороны, продольное волновое число h определяется как частотой (или длиной волны ), так и геометрией поперечного сечения.