Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 39

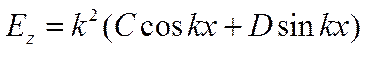
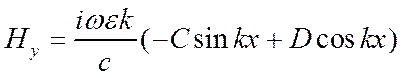
Учтем ГУ на подложке

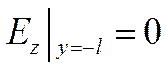
Откуда

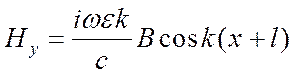
Приравняем касательные компоненты ЭМП на границе раздела ЧО при

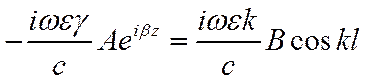
Разделив уравнения друг на друга, получим ДУ

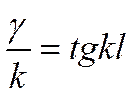
или

Т.к. 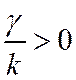, то . Гребенка обладает свойствами полосового фильтра

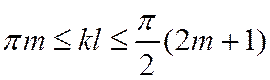
В первой полосе пропускания (m=0) ДХ описывается уравнением

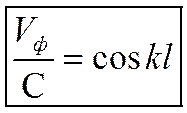
В этом случае распространение МВ возможно только при

.

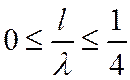Физически это связано с тем, что входное сопротивление короткозамкнутого четвертьволнового отрезка линии, образованной двумя соседними пластинами, равно нулю. Поле не чувствует периодичности ЗС.

9. Применение вариационных принципов для расчета ЗС

Условие равенства эл. и магн. энергии в ячейке ЗС

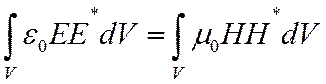                                                       (1)

Исключив Е или Н с помощью УМ, получим выражение для частоты

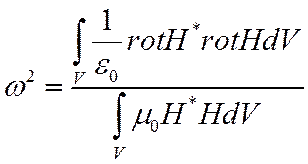
или                                                                                                                   (2)

                                               

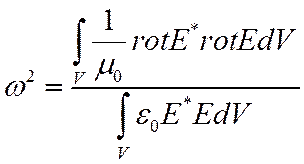
Это – строгие выражения для частоты, если Е и Н – истинные поля.

Их же можно рассматривать как функционалы, определенные на классе непрерывных функций (пробные функции), имеющих непрерывные производные до второго порядка. Будем считать, что они удовлетворяют условиям Флоке и ГУ.

Пробные функции могут не удовлетворять УМ или волновым уравнениям

                                               

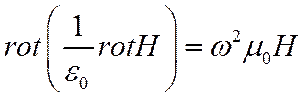
                                                                                                     (3)

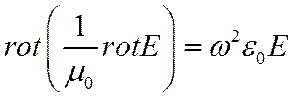
Покажем, что ф-л (2) достигает стационарного значения, если ПФ уд-ют волновому ур-ю (3), т.е. при малых отклонениях ПФ от истинных полей , то ошибка  в определении частоты =0.

Т.е., ошибки в определении частоты имеют второй порядок малости по сравнению с ошибкой в определении поля. Это позволяет при расчете ДХ использовать достаточно грубые приближения при расчете полей без значительного снижения точности результата.

Пусть ПФ удовлетворяют ГУ

                                                                                    (4)

и УФ

                                                (5)                                                  

Умножим обе части (3) на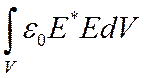

Получим

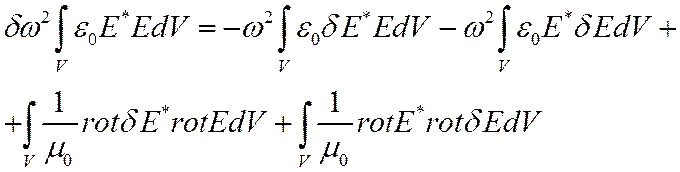
Т.к. 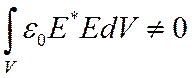, то для выполнения условия , то правая часть уравнения должна обращаться в 0, если ПФ удовлетворяют волновому уравнению, ГУ и УФ.

Учитывая векторное тождество

запишем

 

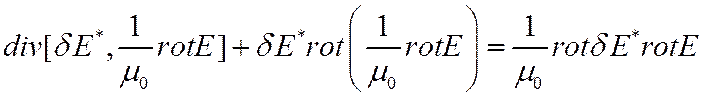
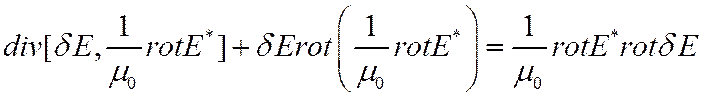
Воспользовавшись т. Остроградского-Гаусса, получим

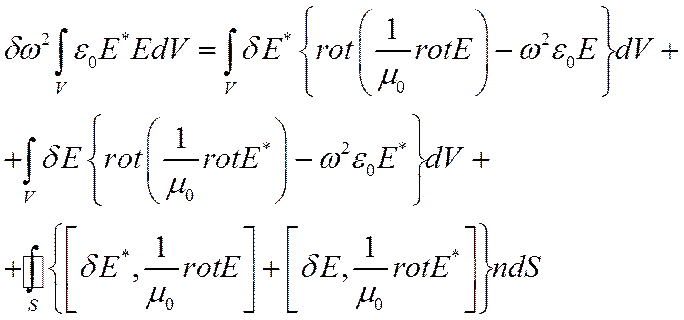
Преобразуем выражение под знаком поверхностного интеграла

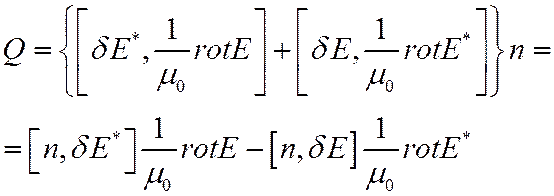                                (6)

Согласно (3) объемные интегралы в правой части =0.

Рассмотрим поверхностные интегралы. Разобьем поверхность ячейки S на S1, S2 и S3. Первые две – это сечения ячейки плоскостями z=const, отстоящими друг от друга на период р. Третья – часть поверхности, ограниченная металлом, в силу ГУ, как это следует из (6),  интеграл по ней =0.

Таким образом,

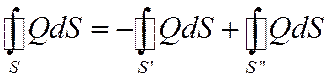
Знак минус связан с тем, что нормали на S’ и S’’ направлены в разные стороны.

Учитывая УФ (4), получим, что пов. интеграл =0.

Т.о. доказано, что функционал достигает своего стац. значения, если ПФ уд-ют волновому ур-ю.

Вместо (2) можно варьировать ф-л

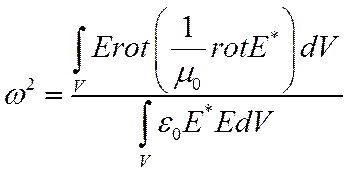                                                              (7)

Он получается из 2 с учетом

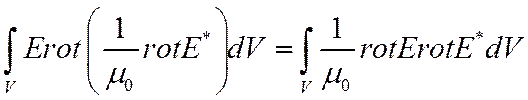
Можно составить ф-л, для которого ПФ не обязаны уд-ть ГУ. Это т.н. ф-лы с естественными ГУ. Для этого в исходный ф-л, например (7), добавляют слагаемые, которые сокращаются с пов. интегралами при варьировании

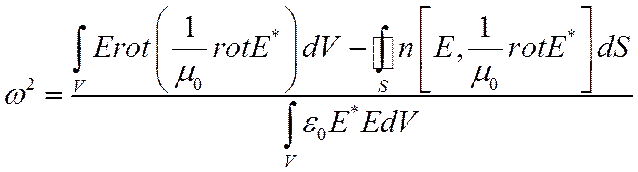                              (8)

Но сходимость при применении численных методов для таких ф-лов хуже.

Метод малых возмущений.

Как изменится собственная частота резонатора при небольших деформациях поверхности или при помещении внутрь металлических или диэлектрических тел.

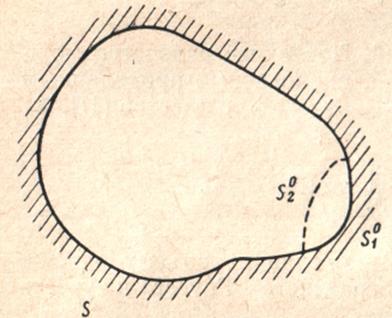
Рассмотрим резонатор с поверхностью S+S1. Его частота определяется (7).