Воспользуемся формулой для
волнового сопротивления диполя в свободном пространстве  и
для соотношения сопротивлений
и
для соотношения сопротивлений ![]() найдем выражение
найдем выражение
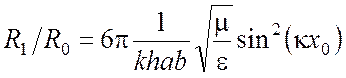 .
(6.57)
.
(6.57)
 |
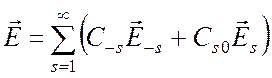 ,
,
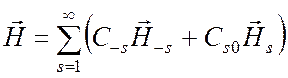 (при - L < z < z1), (6.58)
(при - L < z < z1), (6.58)
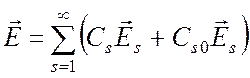 ,
,
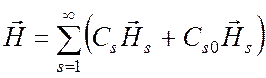 (при z
> z2), (6.59)
(при z
> z2), (6.59)
где ![]() - есть коэффициент отражения
волны от перегородки при z = - L. Заметим, что отраженная волна присутствует как слева
от источников, так и справа.
- есть коэффициент отражения
волны от перегородки при z = - L. Заметим, что отраженная волна присутствует как слева
от источников, так и справа.
Найдем коэффициент отражения ![]() из граничных условий. Считая, что на
перегородке выполняются идеальные граничные условия Еt = 0 при z =
- L и пользуясь формулой (6.34) для
из граничных условий. Считая, что на
перегородке выполняются идеальные граничные условия Еt = 0 при z =
- L и пользуясь формулой (6.34) для ![]() получаем выражение
получаем выражение
![]() (6.60)
(6.60)
Поэтому полное поле справа от источников (при z > z2) имеет вид
 ,
,
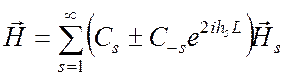 ,
(6.61)
,
(6.61)
Пусть возбуждается только 1
- ая волна. Тогда, учитывая, что ![]() , можно представить
мощность излучения
, можно представить
мощность излучения ![]() для волны ТМ в виде
для волны ТМ в виде
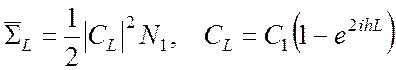 ,
,
или
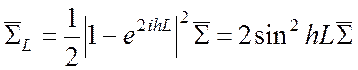 ,
(6.62)
,
(6.62)
где ![]() - мощность излучения в
бесконечном волноводе. Соответствующее сопротивление излучения равно
- мощность излучения в
бесконечном волноводе. Соответствующее сопротивление излучения равно
RL = 2R sin2 hL.(6.63)
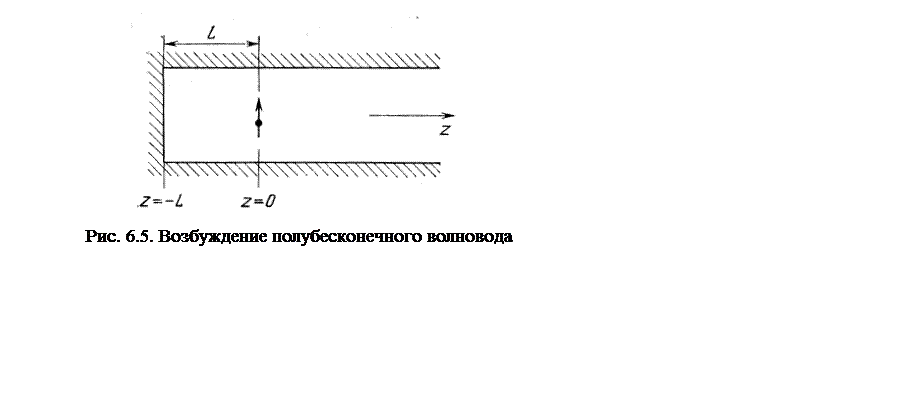
 Задачу о возбуждении полубесконечного
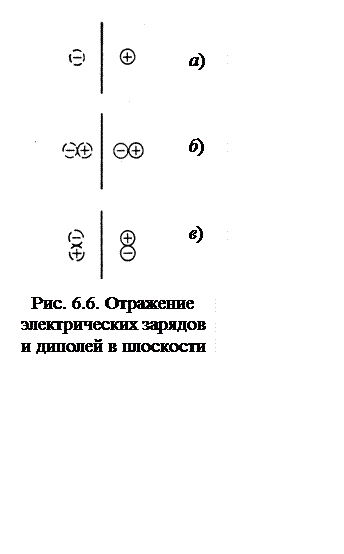
волновода можно решить также методом изображений. Из электростатики известно,
что поле заряда над проводящей плоскостью эквивалентно полю заряда и его
зеркального изображения в свободном пространстве (рис. 6.6,а). Отсюда
вытекают законы отражения для электростатических диполей - нормального к
плоскости (рис. 6.6,б) и параллельного ей (рис. 6.6,в). Если плоскость обладает идеальной
проводимостью, то эти законы отражения применимы и в электродинамике. Они
также обобщаются на случай, когда идеально проводящая плоскость перегораживает
волновод, как на рис. 6.5. Поэтому электромагнитное поле в волноводе,
показанном на рис. 6.5., совпадает при z > -L с электромагнитным полем,
возбуждаемым в бесконечном волноводе двумя диполями: в точке х = х0,
у = у0, z = 0 и в точке х
= х0, у = у0, z = - 2L, причем второй диполь является
зеркальным изображением реального диполя (первого) в плоскости z = - L.
Задачу о возбуждении полубесконечного
волновода можно решить также методом изображений. Из электростатики известно,
что поле заряда над проводящей плоскостью эквивалентно полю заряда и его
зеркального изображения в свободном пространстве (рис. 6.6,а). Отсюда
вытекают законы отражения для электростатических диполей - нормального к
плоскости (рис. 6.6,б) и параллельного ей (рис. 6.6,в). Если плоскость обладает идеальной
проводимостью, то эти законы отражения применимы и в электродинамике. Они
также обобщаются на случай, когда идеально проводящая плоскость перегораживает
волновод, как на рис. 6.5. Поэтому электромагнитное поле в волноводе,
показанном на рис. 6.5., совпадает при z > -L с электромагнитным полем,
возбуждаемым в бесконечном волноводе двумя диполями: в точке х = х0,
у = у0, z = 0 и в точке х
= х0, у = у0, z = - 2L, причем второй диполь является
зеркальным изображением реального диполя (первого) в плоскости z = - L.
Развитая выше теория возбуждения волн заданными источниками может быть применена для решения большого числа электродинамических задач. Эта теория также легко обобщается на другие, более сложные, системы. Так, например, соответствующие соотношения лишь с незначительными изменениями переносятся на передающие линии, имеющие периодическую структуру.
Работа большинства электронных
СВЧ усилителей и генераторов основана на взаимодействии электронного потока и
СВЧ поля, в результате которого электронный поток передает часть своей энергии
полю. Для осуществления указанного взаимодействия необходимо обеспечить в
течение длительного времени (по сравнению с периодом колебаний) условие
синхронизма ![]() , где
, где ![]() – фазовая
скорость волны,
– фазовая
скорость волны, ![]() – скорость электронного пучка. В
силу того, что
– скорость электронного пучка. В
силу того, что ![]() всегда меньше скорости света
всегда меньше скорости света ![]() , условие синхронизма может быть выполнено
только для медленных волн.
, условие синхронизма может быть выполнено
только для медленных волн.
Существует несколько способов
замедления волн. Так, например, медленные волны могут распространяться в
рассмотренных ранее регулярных волноводах при их заполнении диэлектриком. При
этом коэффициент замедления вдали от критической частоты 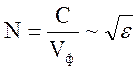 . Поэтому данный способ практически
непригоден для замедления волн в десятки раз.
. Поэтому данный способ практически
непригоден для замедления волн в десятки раз.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.