Вследствие возрастания ![]() при
при ![]()
![]() l
и
l
и ![]()
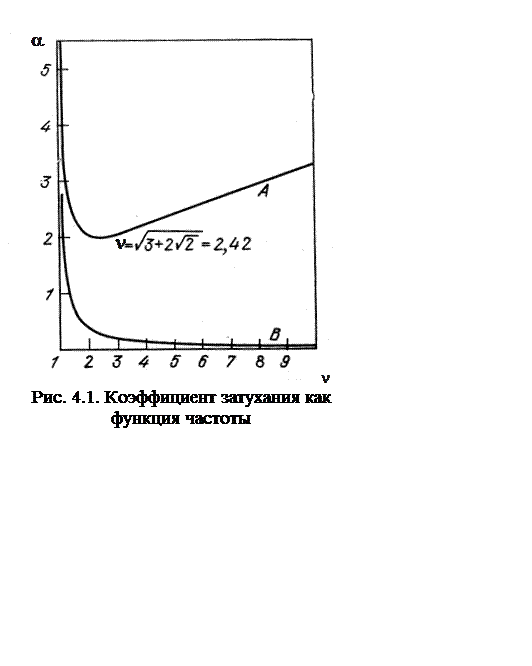
![]() зависимость коэффициента
затухания от частоты имеет характер кривой А на рис. 4.1. Эта кривая
имеет один минимум при
зависимость коэффициента
затухания от частоты имеет характер кривой А на рис. 4.1. Эта кривая
имеет один минимум при ![]() > l.
> l.
 Затухание электрических волн всегда
представляется кривыми качественно того же вида, что и кривая А на рис.
4.1. Однако затухание некоторых магнитных волн может изменяться и по кривой вида В. Этот исключительный случай
имеет место при C1 = 0, когда формула (4.32)
принимает вид
Затухание электрических волн всегда
представляется кривыми качественно того же вида, что и кривая А на рис.
4.1. Однако затухание некоторых магнитных волн может изменяться и по кривой вида В. Этот исключительный случай
имеет место при C1 = 0, когда формула (4.32)
принимает вид
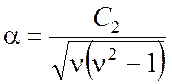 .
(4.33)
.
(4.33)
В этом случае при увеличении частоты затухание быстро
спадает: при ![]()
![]() l
имеем
l
имеем  . Как видно из формулы (4.23), условие
C1 = 0 влечет за собой равенство
. Как видно из формулы (4.23), условие
C1 = 0 влечет за собой равенство
 ,
,
что возможно лишь при
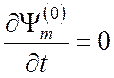 или
или ![]() = const на С. (4.35)
= const на С. (4.35)
Таким образом, затухание
представляется кривой вида В лишь для магнитной волны, функция ![]() которой постоянна на граничном контуре С.
В прямоугольном волноводе согласно общей формуле (3.28) такой волны нет,
но в круглом волноводе она существует; это - волна Н01
функция
которой постоянна на граничном контуре С.
В прямоугольном волноводе согласно общей формуле (3.28) такой волны нет,
но в круглом волноводе она существует; это - волна Н01
функция ![]() которой определяется формулой (3.43), а
также волны Н02, Н03 и т. д.
которой определяется формулой (3.43), а
также волны Н02, Н03 и т. д.
Заметим, что соотношение (4.35)
показывает, что у данной магнитной волны продольные токи равны нулю. Физическое
отличие волны Н01 в круглом волноводе, приводящее к
аномально малым затуханиям, заключается именно в отсутствии у нее продольных
токов. Наличие продольных токов у всех других волн ведет к тому, что затухание
при ![]() >> l возрастает пропорционально
>> l возрастает пропорционально ![]() .
.
Выведем расчетную формулу для
коэффициента затухания волны Н10 в прямоугольном волноводе,
применяемом обычно для передачи сантиметровых радиоволн. Для этого
воспользуемся формулой (4.23) и подставим в (4.28) выражение для ![]() согласно (3.32)
согласно (3.32)
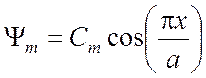 ,
, 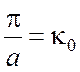 .
.
Напомним, что через а и b обозначены стороны прямоугольного сечения волновода.
Пользуясь соотношениями
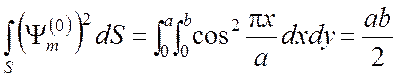 ,
, 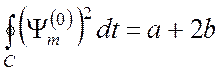 ,
,
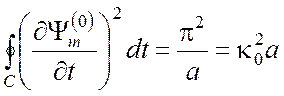 ,
,
получим
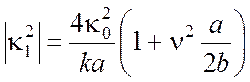 .
(4.36)
.
(4.36)
Так что
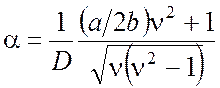 ,
,
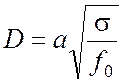 . (4.37)
. (4.37)
Через ![]() здесь обозначена
критическая частота волны Н10 (
здесь обозначена
критическая частота волны Н10 (![]() ),
поэтому
),
поэтому
![]() .
(4.38)
.
(4.38)
В последнюю формулу нужно подставлять значение ![]() , Ом-1см-1. Ширину а
нужно выражать в сантиметрах, тогда величина
, Ом-1см-1. Ширину а
нужно выражать в сантиметрах, тогда величина ![]() имеющая
размерность длины, также получается в сантиметрах.
имеющая
размерность длины, также получается в сантиметрах.
Кривая А на рис. 4.1
построена по формуле (4.37) для волны Н10 в прямоугольном
волноводе, большая сторона которого вдвое шире
меньшей (а = 2b). Видно,
что минимальное затухание достигается при ![]() = 2,42,
причем минимум является довольно пологим. Рабочий диапазон частот обычно
выбирают слева от этого минимума (при
= 2,42,
причем минимум является довольно пологим. Рабочий диапазон частот обычно
выбирают слева от этого минимума (при ![]() < 2),
поскольку при
< 2),
поскольку при ![]() > 2 появляются распространяющиеся
волны Н01 и Н20, в сильной степени
усложняющие свойства волновода как передающей линии.
> 2 появляются распространяющиеся
волны Н01 и Н20, в сильной степени
усложняющие свойства волновода как передающей линии.
Оценим теперь порядок величины D в формуле (4.37). Для этого
положим а = 2 см, b = 1 см, что примерно
соответствует размерам стандартного прямоугольного волновода для трехсантиметрового
диапазона волн, и возьмем медный волновод с проводимостью стенок ![]() = 5-10 -17 с-1. В
этом случае
= 5-10 -17 с-1. В
этом случае
![]() = 7,5.109 Гц, D
= 7,5.109 Гц, D ![]() 2-104 см = 200 м.
2-104 см = 200 м.
Поэтому вблизи минимума затухания на рис. 4.1 (где ![]() ) электромагнитное поле волны Н10
ослабляется в е раз при передаче на расстояния порядка 100 м. При
увеличении рабочей длины волны и соответственном расширении поперечных
габаритов волновода дальность передачи по волноводу увеличивается, так как
длина D пропорциональна а3/2.
) электромагнитное поле волны Н10
ослабляется в е раз при передаче на расстояния порядка 100 м. При
увеличении рабочей длины волны и соответственном расширении поперечных
габаритов волновода дальность передачи по волноводу увеличивается, так как
длина D пропорциональна а3/2.
Как было отмечено ранее, почти все волны в волноводах имеют качественно такую же зависимость затухания от частоты, что и волна Н10 в прямоугольном волноводе (кривая А на рис. 4.1). Исключение составляет волна Н01 (а также волны Н02, Н03, ...) в круглом волноводе, затухание которой с ростом частоты неограниченно падает. Для этой волны согласно формуле (3.43) нужно взять
![]() ,
, ![]() ,
, ![]() = 3,832;
= 3,832;
Тогда
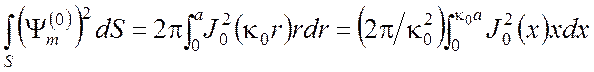 ,
, 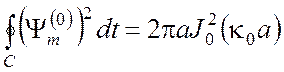 ,
,
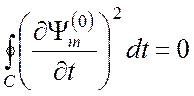
Известное соотношение теории бесселевых функций
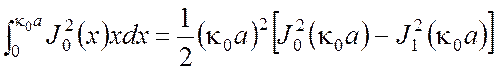
в данном случае упрощается в силу того, что ![]() . По формуле (4.23) получаем
. По формуле (4.23) получаем
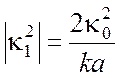 ,
(4.39)
,
(4.39)
так что коэффициент затухания волны Н01 в круглом волноводе можно записать в виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.