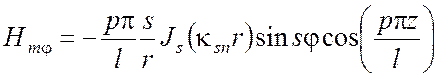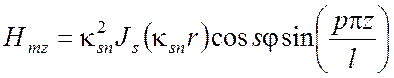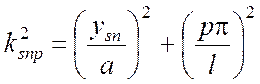Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 25

, ,

.                                      (5.30)

Волны в резонаторе определяются колебаниями Е_sпp и H_sпp, причем в цилиндрических резонаторах колебания Е_sп0 существуют, а колебания Н_sп0 отсутствуют. Формула (5.28) показывает, что собственная частота колебания Е_sп0 совпадает с критической частотой волны Е_тп в волноводе (). Собственные частоты всех других коле­баний E_snq (или H_snq) выше критических частот соответствующих волн Е_sп (или Н_sп)в волноводе.

Как уже отмечалось в § 5.2, основным колебанием резонатора называется колебание с наименьшей собственной частотой. Из фор­мул (5.28) и (5.30) следует, что для длинных резонаторов (l велико) основным колебанием будет магнитная стоячая волна с индексом p = 1.Для коротких резонаторов (l мало) основным колебанием будет электрическая стоячая волна с индексом  p = 0, по­скольку при p  0 второе слагаемое в формулах (5.28) и (5.30) будет большим. Так, для кругового цилиндра основным колебанием может быть либо колебание Е₀₁₀  с волновым числом k = 2,405/a, либо колебание Н₁₁₁ с волновым числом

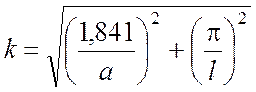.                                (5.31)

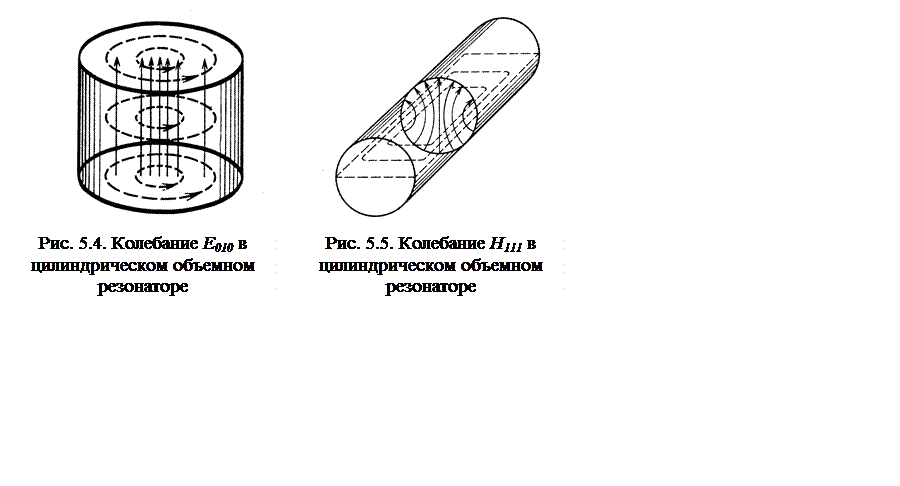
Собственные частоты этих колебаний совпадают при . При больших отношениях  колебание Н₁₁₁ является основным, причем его частота является двукратной. При меньших отношениях основным бу­дет колебание Е₀₁₀, частоту которого нетрудно вычислить по фор­муле k = 2,405/a. Эта частота не зависит от длины резонатора l и является невырожденной. Обычно в цилиндрических резонато­рах применяется колебание Е₀₁₀, причем l  < 2а. На рис. 5.4 и 5.5 изображено распределение электрических (сплошных) и магнит­ных (штриховых) силовых линий в цилиндрическом резонаторе при колебаниях Е₀₁₀ и Н₁₁₁.

5.4. Влияние конечной проводимости стенок на свободные колебания резонатора

Если не учитывать конечную проводимость стенок резонатора и использовать идеальные граничные условия, то получаем незатухающие колебания.  Учет конечной проводимости стенок приводит к тому, что свободные колебания в пустых резонаторах затухают вследствие потерь в стенках. Найдем коэффициент затухания и воспользуемся для этого энергетическим методом.

Вследствие затухания частоты свободных колебаний являются слегка комплексными , где  - резонансная частота резонатора, частота  - имеет смысл коэффициента затухания. Это значит, что мгновенные значения полей затухают по экспоненциальному закону (пропорционально), а энергия электромагнитного поля в резона­торе - по закону

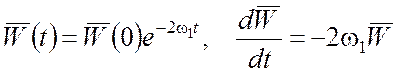.                        (5.32)

Найдем приближенное значение коэффициента затухания , воспользовавшись законом сохранения энергии (1.11), усред­нив его по периоду колебания:

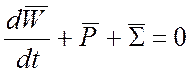,                                           (5.33)

где усреднение обозначено чертой сверху. Этот закон удобно применить к объему резонатора V, ограниченному поверхностью стенки S. Токи в стенке расположены вне объема, поэтому . Сочетая формулы (5.32) и (5.33), получаем коэффициент затухания в виде

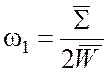.                                                    (5.34)

Величину   - среднюю мощность, вытекающую из объема и поступающую в стенку резонатора, вычислим приближенно с помощью условия Леонтовича (4.8)

,

где  t  отождествляется с тангенциальным магнитным полем на стенке идеального резонатора.

Тогда имеем

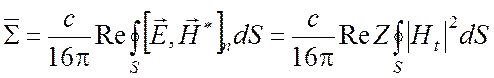.                              (5.35)

Энергетическая формула (5.35) применяется обычно для приближенных расчетов, исходя из тех полей, которые найдены в предположении об идеальной проводимости стенок. Средняя энергия поля также вычисляется для идеального резонатора, причем считаем, что сред­нее значение электрической энергии равно среднему значению магнитной энергии, поэтому полная энергия  равна удвоенной средней магнитной энергии

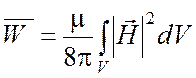.                               (5.36)

В результате для коэффициента затухания получаем

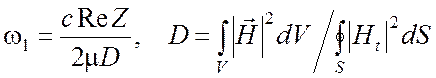.                        (5.37)

Выразим волновое сопротивление Z через глубину скин – слоя d и, учитывая, что проводимость стенок велика (4.25) в результате получаем

.

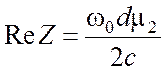И, окончательно,