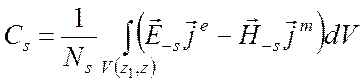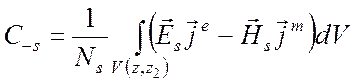Основные положения теории электромагнитного поля. Плоские электромагнитные волны. Волны в регулярном волноводе. Потери в волноводах. Возбуждение электромагнитных волн, страница 32

, ,     (6.45)

где скобка (z₁, z) означает, что интегрирование производится по всем источникам левее данного сечения z, а скобка (z, z₂) - ин­тегрирование по всем источникам правее сечения z.

Однако поле  отличается от поля , существующего в том же сечении до удаления источников: удаляя источники из слоя, тем самым обрываем продольные электрические и магнит­ные токи и создаем на поперечных сечениях z -  и z +  поверхностные электрические и магнитные заряды. На сечении z -  по­верхностные плотности электрического заряда и магнитного за­ряда связаны с продольными составляющими j^e_z и j^m_z соотно­шениями

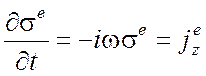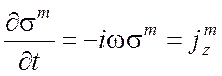, .      (6.46)

В сечении z +  плотности поверхностных зарядов равны соот­ветственно - и -. Поверхностные  заряды  создают  в  слое (z - , z + ) при  дополнительное поле

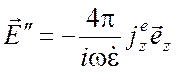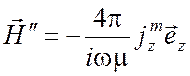, .                             (6.47)

Так как поле , получаемое по формулам (6.25) и (6.45), есть поле в «препарированном» поперечном сечении (рис. 6.4,б), а поле  возникает в результате «препарирования», то для оп­ределения поля, существующего в реальной системе (рис. 6.4,а), необходимо из первого поля вычесть второе. Таким образом, окончательные выражения для искомого электромагнитного поля имеют вид

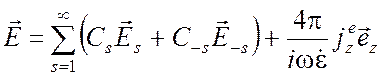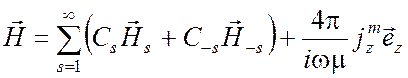,    , (6.48)

где коэффициенты C_s и C_-s даются формулами (6.45). При z₁ < z < z₂ эти коэффициенты являются функциями от z, так как при изменении z «левые» источники превращаются в «правые» (или наоборот) и вследствие этого амплитуды волн изменяются.

Вне области, занятой источниками, дополнительные слагаемые в формулах (6.48) пропадают, коэффициенты C_s и C_-s  перестают зависеть от z, и формулы (6.48) переходят в формулы (6.40) и (6.41). Поэтому выражения (6.48) и (6.45) дают самую общую запись электромагнитного поля, возбужденного в волноводе заданными источниками.

Рассмотрим возбуждение электромагнитных волн рамочными антеннами, щелями и отверстиями. В частности, если волновод возбуждается с помощью отверстия в его идеально проводящей стен­ке S₀, то формулы (6.44) принимают вид

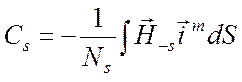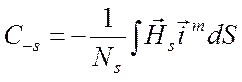, ,                 (6.49)

где вследствие поверхностного характера магнитного тока интег­ралы распространяются по площади отверстия (или щели).

Поверхност­ные электрические токи вводятся по формуле (1.31), а магнитные токи – по аналогичной, полученной по принципу перестановочной двойственности. Это происходит тогда, когда рассматриваемое электромагнитное поле претерпевает разрыв на некоторой поверхности S. Так, если электро­магнитное поле принимает значения  на стороне 1 поверх­ности S и равно нулю на стороне 2 этой поверхности, то формулы (1.31) принимают вид

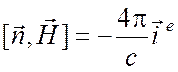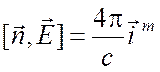,    .                    (6.50)

Таким образом, данному разрывному полю соответствуют элект­рические и магнитные поверхностные токи. Формулы (6.50) остаются в силе, если S есть поверхность идеального проводника. Тогда в силу граничного условия (6.22) поверхностные магнитные токи на S.

В электродинамике рассматривают задачи об излучении из от­верстий и щелей, прорезанных в металлических поверхностях, ко­торые считают идеально проводящими. Часто тангенциальное эле­ктрическое поле на отверстии или на щели можно считать извест­ным, а на металлической поверхности оно равно нулю. Если в лемме (6.5) сначала задать на идеально проводящей поверх­ности S₀ (части поверхности S) тангенциальное поле , а по­том плотность поверхностного тока  (предельный случай плот­ности ), а поле  брать одним и тем же, то придем к соотношению

,

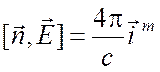совпадающему со вторым соотношением (6.50). При выводе предполагается, что отверстие или щель как бы заметаллизированы, т. е. имеется сплошная идеально проводящая поверхность S₀ без вырезов, которой и соответствует вспомогательное поле .

Поль­зуясь этим соотношением, преобразуем формулы (6.49) к виду

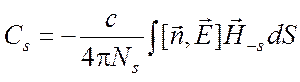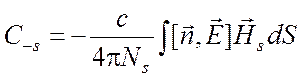, ,               (6.51)

где  есть электрическое поле на отверстии.  Иначе можно на­писать

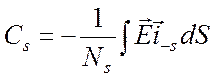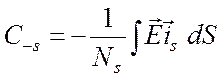 , ,                            (6.52)

где

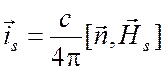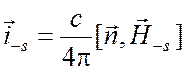,                               (6.53)