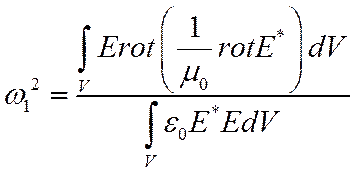 (9)
(9)
Если часть стенки S1 деформировать до S2, то частота изменится с w1 до w2.
Определим w2 с помощью (8) взяв в качестве ПФ истинное поле для исходного р-ра.
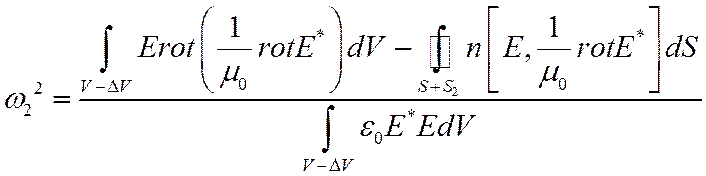 (10)
(10)
Поверхностный интеграл отличен от 0 только на поверхности S2, т.к. ф-я E удовлетворяет ГУ на S. Вычтем (9) из (10), отбрасывая в знаменателе малые
слагаемые по ср. с 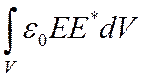
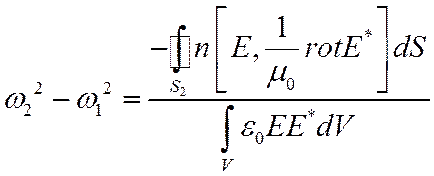 (11)
(11)
Заменим интеграл по S2 на на интеграл по замкнутой пов-ти S1+S2, учитывая, что в силу ГУ инт. по S1 равен 0.
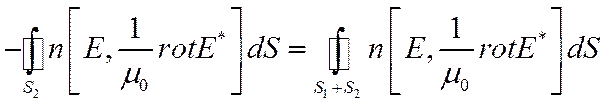
Знак минус – из-за изменения направления нормали.
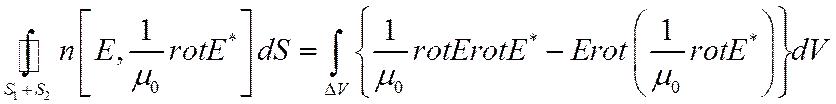
Отсюда следует
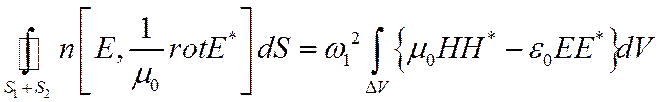
Подставляя это в (11), и полагая 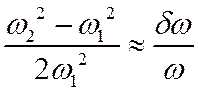 получим
получим
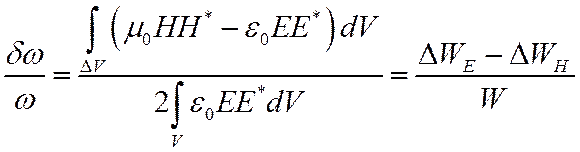
Эта же ф-ла м.б. использована и в более общем случае. Например, для определения изменения собственной частоты р-ра при внесении разл возмущающих тел
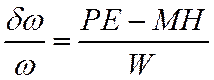
Р и М – электрический и магнитный моменты возмущающих тел.
Приложение 1
В криволинейной системе координат
(![]() ) квадрат элемента длины
) квадрат элемента длины ![]() и элемент объема
и элемент объема ![]() выражаются
формулами
выражаются
формулами ![]() и
и ![]() соответственно,
где
соответственно,
где ![]() - параметры Ламэ.
- параметры Ламэ.
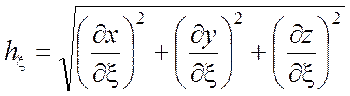 (П1.1)
(П1.1)
- параметр Ламэ по координате ![]() .
Параметры Ламэ
.
Параметры Ламэ ![]() и
и ![]() определяются
аналогично (П1.1).
определяются
аналогично (П1.1).
Градиент функции ![]()
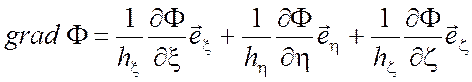 ,
(П1.2)
,
(П1.2)
где ![]() ,
, ![]() , и
, и ![]() - единичные орты в направлении
координатных осей
- единичные орты в направлении
координатных осей ![]() и
и ![]() .
Дивергенция вектора
.
Дивергенция вектора ![]()
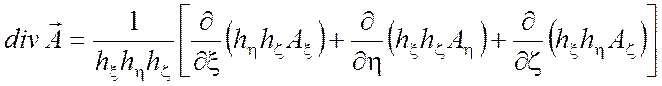 (П1.3)
(П1.3)
Ротор вектора ![]()
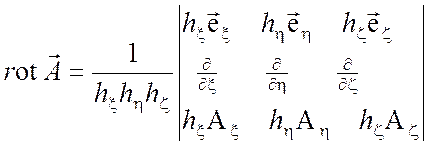 (П1.4)
(П1.4)
Оператор Лапласа (Лапласиан)
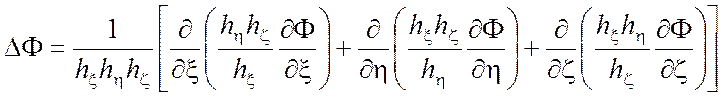 (П1.5)
(П1.5)
Часто встречающиеся тождества и соотношения:
Ротор ротора ![]() (П1.6)
(П1.6)
Ротор градиента ![]() (П1.7)
(П1.7)
Дивергенция ротора ![]() (П1.8)
(П1.8)
Дивергенция градиента ![]() (П1.9)
(П1.9)
Выражения градиента, дивергенции, ротора и оператора Лапласа в декартовой системе координат (x, y, z):
![]()
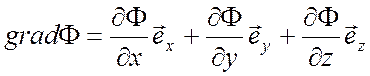 (П1.10)
(П1.10)
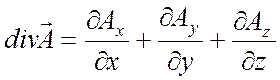
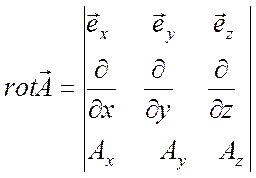
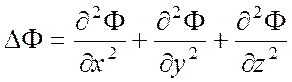
Выражения градиента, дивергенции,
ротора и оператора Лапласа в цилиндрической системе координат ![]() :
:
![]()
![]()
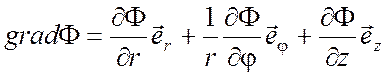 (П1.11)
(П1.11)
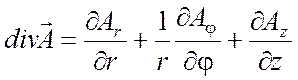 (П1.12)
(П1.12)
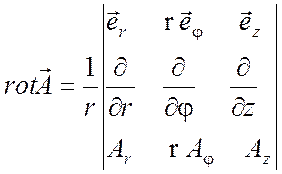 (П1.13)
(П1.13)
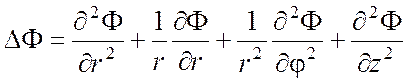 (П1.14)
(П1.14)
Оператор Лапласа от вектора определяется в соответствии с формулой (П1.6) и имеет вид
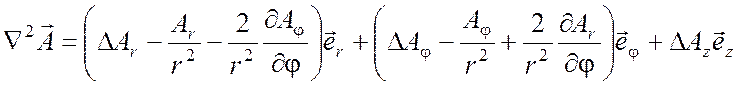 (П1.15)
(П1.15)
Выражения градиента, дивергенции,
ротора и оператора Лапласа в сферической системе координат ![]()
![]()
![]()
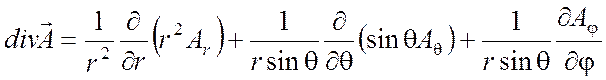 (П1.16)
(П1.16)
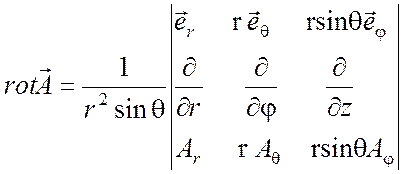 (П1.17)
(П1.17)
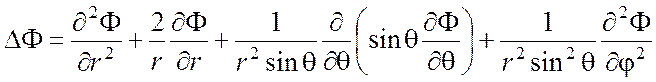 (П1.18)
(П1.18)
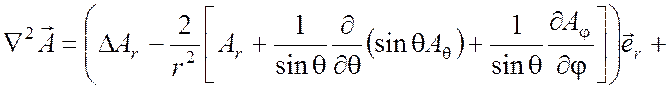 (П1.19)
(П1.19)
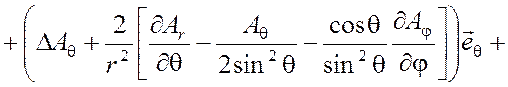
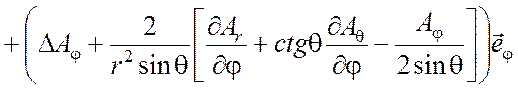 .
.
Интегральная формула Грина:
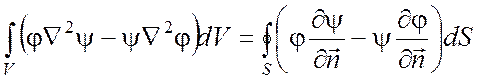 ,
(П1.20)
,
(П1.20)
где S – замкнутая поверхность,
ограничивающая объем V, а ![]() - внешняя нормаль к этой
поверхности.
- внешняя нормаль к этой
поверхности.
Формула Гаусса – Остроградского
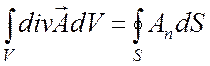 (П1.21)
(П1.21)
Приложение 2
Цилиндрические функции являются решениями уравнения Бесселя
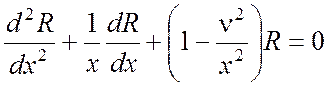 ,
(П2.1)
,
(П2.1)
и называются функциями Бесселя порядка ![]() . Подставляя решение в виде степенного
ряда типа
. Подставляя решение в виде степенного
ряда типа 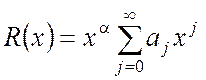 , находим, что
, находим, что ![]() и
и 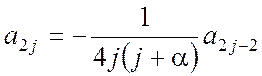 при j = 0,
1, …. Коэффициенты при всех нечетных степенях
при j = 0,
1, …. Коэффициенты при всех нечетных степенях ![]() равны
нулю. Воспользовавшись итерацией рекуррентной формулы, приходим к следующему
выражению для функции Бесселя, или цилиндрической функции первого рода, порядка
равны
нулю. Воспользовавшись итерацией рекуррентной формулы, приходим к следующему
выражению для функции Бесселя, или цилиндрической функции первого рода, порядка
![]() и
и ![]() :
:
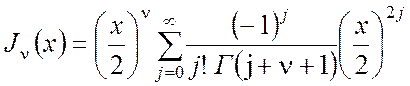 ,
(П2.2а)
,
(П2.2а)
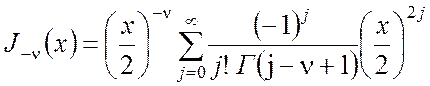 ,
(П2.2б)
,
(П2.2б)
где ![]() - гамма – функция, которая для Re s
> 0 определяется формулой
- гамма – функция, которая для Re s
> 0 определяется формулой
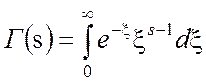 (П2.3)
(П2.3)
Основные свойства гамма – функции
![]() ,
,
![]() ,
, ![]() (П2.4)
(П2.4)
Если n
– целое, то из соотношений (3.8) следует ![]() .
.
Если ![]() не
целое число, то функции
не
целое число, то функции ![]() и
и ![]() образуют пару линейно – независимых
решений дифференциального уравнения (П2.1). Однако при целых
образуют пару линейно – независимых
решений дифференциального уравнения (П2.1). Однако при целых ![]() эти решения, как известно, линейно
зависимы. Действительно, при
эти решения, как известно, линейно
зависимы. Действительно, при ![]() , как видно из
соотношений (П2.2), имеет место соотношение
, как видно из
соотношений (П2.2), имеет место соотношение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.